| Submit | All submissions | Best solutions | Back to list |
GRIDSUM2 - 2x2 Subgrid Sum Problem (hard) |
This problem is a higher constraints version of KWACIK (Polish) and GRIDSUM1.
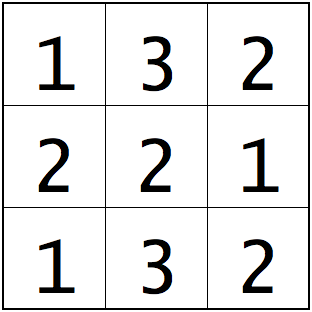
You are given a 3x3 grid. You can place an integer m (a ≤ m ≤ b) in each cell.
How many ways are there to place integers in the cells such that the sum of each 2x2 subgrid is n ?
Since the answer might be very large, output it modulo 108.
Input
The first line contains an integer T (1 ≤ T ≤ 100), the number of test cases.
On each of the next T lines, you are given three integers a, b and n. (0 ≤ a ≤ b ≤ 50000, 0 ≤ n ≤ 200000)
Output
For each test case, output a single line containing the number of ways to place integers modulo 108.
Example
Input:
1 1 2 5
Output:
8
Explanation
There are 8 ways to place integers for a=1, b=2 and n=5.
2 1 2 : 2 1 2 : 2 1 1 : 1 2 1 : 1 2 1 : 1 1 2 : 1 1 1 : 1 1 1 1 1 1 : 1 1 1 : 1 1 2 : 1 1 1 : 1 1 1 : 2 1 1 : 2 1 2 : 1 2 1 2 1 2 : 1 2 1 : 2 1 1 : 2 1 2 : 1 2 1 : 1 1 2 : 1 1 1 : 1 1 1
Credit & Special thanks
- Bartek - the original problem author
- Mitch Schwartz
| Added by: | Min_25 |
| Date: | 2014-10-17 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 GOSU |
| Resource: | KWACIK |


 RSS
RSS