| Submit | All submissions | Best solutions | Back to list |
BFIT - Best Fit |
You are given a sequence of N random values (s1, s2, s3, s4, ... sN) You have to find a function f(t) = a*t+b such that the Euclidean Distance between the given sequence and the function values where t varies from 1 to N is minimum.
In effect, you have to minimize
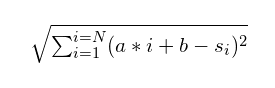
Output the values a and b for each test case, rounded up to 4 decimal places.
Input
Line 1: T /* Number of test cases T <= 1000 */
Line 2: N /* Number of values in first test case N <= 10000 */
Line 3: s1 s2 s3 s4 … sN /* all values are less than 10000 and integers */
.
.
.
Output
a b /* Output the values a and b rounded to 4 decimal places for each test case */
Example
Input: 3
3
1 1 1
3
1 2 3
3
1 3 1 Output: 0.0000 1.0000
1.0000 0.0000
0.0000 1.6667
| Added by: | Shashank Kumar |
| Date: | 2011-04-16 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | INSOMNIA 11 |
hide comments
|
2022-02-21 08:57:23
missing pict: \sqrt{\sum_{i=1}^{i=N}( a*i + b - s_{i})^{2} } Last edit: 2022-02-21 08:57:39 |
|
|
2015-05-08 21:02:52 Dune
the gif file with a formula of the problem's description is missing. |
|
|
2013-05-20 06:22:02 !!.Nginx.!!
Finally AC.....School maths problem..!!! :D Last edit: 2013-05-20 06:50:36 |
|
|
2013-05-17 17:48:24 bashrc is back
answer not fitting in int???i changed int to long long and got AC |
|
|
2013-05-17 17:48:24 Hagen von Eitzen
One may assume that s1, s2, ..., sN are integers |
|
|
2013-05-17 17:48:24 blashyrkh
Least mean square method. O(N). Multiple answers possible only if N==1 (I got AC hence there is no such test cases). |
|
|
2013-05-17 17:48:24 ebd
What if there are multiple answers; any of them is acceptable? |
|
|
2013-05-17 17:48:24 ||zone
1000 test cases, each with 10000 N , how can it be solved even if we get the answer in O(1). thats the max! Last edit: 2011-04-18 04:07:37 |


 RSS
RSS