| Submit | All submissions | Best solutions | Back to list |
ARCHPLG - The Archipelago |
Bytelandian islands are rather small and none are very fertile, so each of (rectangular of course) pieces of cultivated land is under special control, simply speaking: ‘never enter there to save your life’. Other areas are guaranteed to be free accessible for the people.
The communication between islands is possible by ferries. On each island there is 0<=b<=10 terminals, from where crossings to another terminals on other islands are possible. It is known that total number of crossing connections is 0<=m<=100000. Other infrastructure is practically unknown. Specifically the only possible way of traveling through the island is to do it on foot.
Well, now we are close to a task you are requested to solve. John – one of the Bytelandian citizens is working as a sales manager. Simply speaking he is often requested to travel from one place to another, what he rather dislike and preferably (like other Bytelandian people use to do) he would like to spent more time in one of the beach clubs playing Puto (a kind of strategic game, very popular in Byteland). Please help him to find a way to spare his time.
Task
Find one of the fastest ways for John using ferries and foot paths on islands. Assume that while walking John is always moving one BM (Bytelandian unit of length) per BH (Bytelandian unit of time). You can also assume that the ferry departures nearly immediately after John arrives the terminal, it will be enough to round up the walking time to the nearest integer.
Input
In the first line t - the number of tests, then for each test: in next line n - the number of islands. Description of each island is as follows:
name w h [island dimensions] b - [number of terminals] [description of each terminal in a form:] name x y [name of a terminal and its coordinates] F [number of restricted areas F<20] xl, yd, xr, yu [coordinates of each restricted area, 0 <=xl < xr<=250 0<=yd < yu<=250.]
All coordinates are nonnegative integers measured in BM according to upper left corner of an island.
You can assume that any two restricted areas are disjoint. After the description of all islands all ferry connections are given (each connection is bi-directional).
m [number of connections] [description of each connection] NB1 NW1 NB2 NW2 time [name of a first terminal, its island, the second respectively and communiaction time] ... [description follows] ... NBS NWS NBC NWC [start and goal terminal for John]
Output
For each test describe the shortest route for John from terminal NBS on NWS island to terminal NBC on NWC island in the following format:
case nr Y [nr - test number] T [travel time in BH] NBS NWS ... [consecutive terminals] ... NBC NWC [empty line] [consecutive tests]
If two consecutive terminals are located on the same island and John must take some walk you must give all middle point like in an example.
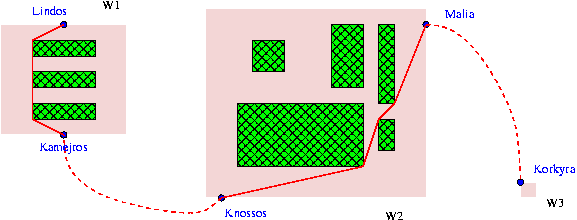
Example
Input: 1 3 W1 8 7 2 Lindos 4 0 Kamejros 4 7 3 2 1 6 2 2 3 6 4 2 5 6 6 W2 14 12 2 Malia 14 1 Knossos 1 12 5 2 6 10 10 11 1 12 6 8 1 10 5 11 7 12 9 3 2 5 4 W3 1 1 1 Korkyra 0 0 0 2 Kamejros W1 Knossos W2 100 Malia W2 Korkyra W3 100 Korkyra W3 Lindos W1
An example of a correct answer:
Output: case 1 Y 230 Korkyra W3 Malia W2 12 6 11 7 10 10 Knossos W2 Kamejros W1 2 6 2 1 Lindos W1
| Added by: | kuszi |
| Date: | 2006-03-15 |
| Time limit: | 5.393s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: NODEJS PERL6 VB.NET |
| Resource: | GUT Algorithm Analysis 2005 |
hide comments
|
2019-08-22 12:16:30 Karolis Kusas
Submitting a solution to this problem gives "Internal error". Could you fix this? :) |
|
|
2019-03-24 22:54:06 kuszi
@weathervane "...the test case has two equal solutions..." Does not matter, all optimum solutions are accepted. |
|
|
2016-11-17 21:29:35
This is a nice question but has some loose ends. It says each farm is disjoint, which means they do not overlap, but may touch. Can John walk between them, or slip through a gap if they touch at the corner? Similarly if a farm touches the island shore, may John walk it? I would guess that is NO to both questions, but more importantly, the test case has two equal solutions - two equal routes on island W1. Does the full challenge also contain such ambiguity? And if so, what is the rule? Last edit: 2016-11-18 09:12:47 |


 RSS
RSS