| Submit | All submissions | Best solutions | Back to list |
APCP1 - Einstein Ring |
Quasars are among the brightest objects in the universe, which may outshine total starlight of their host galaxies! They are believed to be powered by supermassive black holes. Suppose we have a quasar, if there is nothing between it and the Earth, we see one image of the quasar but if a massive galaxy (or cluster of galaxies) is blocking the direct view to the quasar, the light will be bent by the gravitational field around the galaxy (see below diagram). This is called “gravitational lensing” since the gravity of the intervening galaxy acts like a lens to redirect the light rays. But rather than creating a single image of the quasar, the gravitational lens creates multiple images. We follow the light rays from the Earth to the apparent locations of the quasar. If the galaxy were perfectly symmetric with respect to the line between the quasar and the Earth, then we would see a ring of quasars! This deformation of the light from a source into a ring through gravitational lensing of the source’s light by an object with an extremely large Mass is known as “Einstein Ring”.
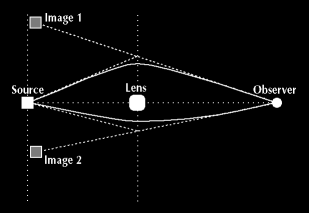
Since the distances between each of the object is so great, the radius of the galaxy and mass distribution of the galaxy is well approximated by point masses. Thus, one can use simple geometry (knowing the mass of the galaxy, the distance of the galaxy and the two images) to estimate the distance to the actual quasar.
In this problem we would be doing something different and further simplify the problem. The Earth and quasar would be taken as point masses. Massive Galaxy in the above diagram is replaced by a vertical straight line. Two images of the quasars are formed as viewed from Earth which are extended indefinitely until they meet the vertical line passing through quasar (line QL in below diagram) this meeting point is to be considered the image point.
Given the length of line ML is “L”, distance of Earth from Massive Galaxy is “Ed”, distance of quasar from the galaxy is “Qd”, Quasar is “d” distance above or below the midpoint of line ML. Positive values of “d” represents above the midpoint and negative values below the midpoint. Two images formed have the name “img1” and “img2” as shown in diagram. You need to find the distance of Quasar from “img1” and “img2” respectively. All distances are without units for the ease of calculation.
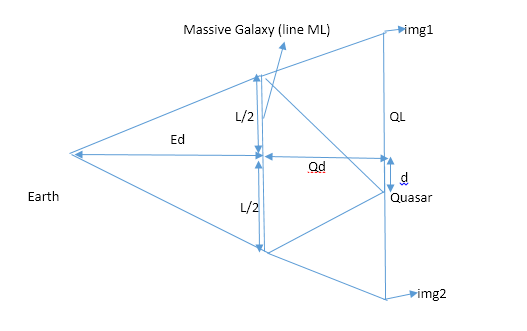
First line of input contains T, 0 < T < 100, representing the number of test cases. T line follows. Each line specifies 4 integers: Ed L Qd d (separated by a space). 0 < Ed, L, Qd < 10^6, -10^6. 0 <= d <= L/2
Output
For every test case Output: two decimal values separated by a space correct up to 6th decimal place representing the absolute distance of Quasar from img1 and img2 respectively.
Example
Input: 2 130 50 80 20 10 5 8 -2 Output: 20.384615 60.384615 6.500000 2.500000
| Added by: | Rishabh Baid |
| Date: | 2013-01-19 |
| Time limit: | 1s-2s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |


 RSS
RSS