SPOJ.com - Problem PROG0482

PROG0482 - Feathered friends

The greater honeyguide (Indicator indicator) living in Africa is obsessed with beeswax, but is not always able to penetrate a hive on his own. Therefore, he has forged a unique partnership with man. The bird attracts the attention of local honey hunters with his rattling cry, flies in the direction of a beehive and regularly stops to cry again. When they reach the hive, the hunter breaks it open, intoxicates the bees with smoke, takes the honey out and leaves the wax for the bird.

This collaboration saves man an average of 5.7 hours of time to find beehives but it is not infallible. "The greater honeyguide has also brought us to the edge of an abyss and to a male elephant", reported biologists Lester Short and Jennifer Horne. "In those cases, there were beehives at the bottom of the cliff (in a valley) and behind the elephant. The welfare of the escorted persons is none of the greater honeyguide's concern."

Assignment

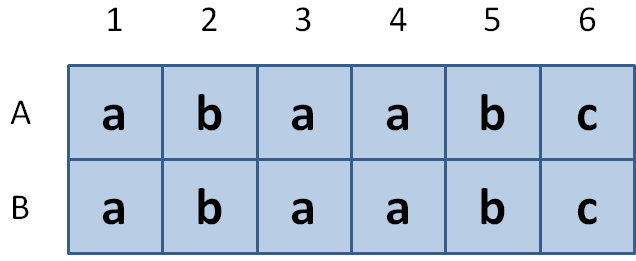
A group of biologists is mapping beehives in the Kenyan savanna, following the bird call of the greater honeyguide. If they have been guided to a hive, they indicate the location of the hive on a rectangular map. The map is divided into square areas. As shown in the example below, the rows of the map are labeled top to bottom with the uppercase letters A, B, …, and the columns from left to right with the numbers 1, 2, 3, …. The square areas are labeled with lowercase letters indicating the types of vegetation as landmarks in the savannah.

When the biologists find a hive with the help of the honeyguide, they have no idea of the position on the map where they left. Fortunately, they have a good sense of direction and can reconstruct the route they have traveled as a sequence of observations and movements.

A route can be described as a string, in which observations are indicated by lowercase letters that describe the type of vegetation and movements by uppercase letters that indicate the direction: L for left, R for right, U for up and D for down. Observations and movements always alternate in the description of the route, and the description always starts and ends with an observation. If the execution of a movement would lead to a square outside the map, the movement is not performed and one stays at the same position.

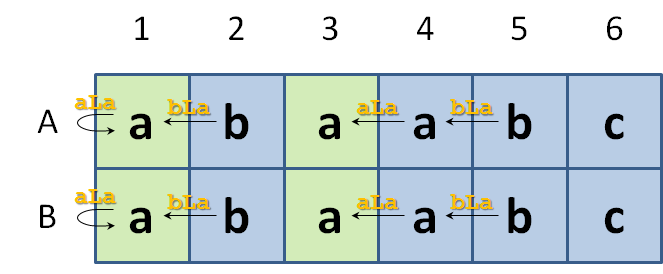
Your task is to find all possible positions on the map where a given route may end. These indicate the possible positions of the beehives. Suppose we need to find every position on the above map where we can end up when following the route bLaLa. The possible end positions, and the corresponding routes are shown in the figure below.

In columns 2 and 5 there is always a lowercase letter b, and therefore the route can start there. If we move to the left from the starting positions, then we always arrive at a square that is labeled with the letter a. So we can continue to follow the route. If we move to the left again, the routes that started at column 5 finish at a square in column 3. These position all have a letter a, so we have been following the route completely. The squares in column 3 are therefore possible end positions. The routes that started at column 2 end after one movement at column 1. If we were to move left again, we would drop outside the map. We therefore stay put, but end up at a square with the letter a. Again, in those cases we have been able to follow the route completely and the squares in column 1 are possible end positions.

The biologists indicate the position of a square on the map with a label (a string) which consists of the row label followed by the column label. In Python, however, it is customary to index rows top to bottom and columns left to right with integers, each time starting from zero. Therefore, first write the following two functions:

A function coord2label that returns the label corresponding to the given row and column index (two separate arguments).
A function label2coord that returns the row and column index (as a tuple) corresponding to the given label.

You may assume that the number of rows on the map never exceeds 26. Now, use the above functions to implement the following three functions.

Write a function observation that takes three arguments: i) the number of rows in a rectangular map, ii) a string of lowercase letters that indicate the labels of the squares on the map, read from left to right and from top to bottom, and iii) the label of a square on the map. The function must return the lowercase letter at the square of the map indicated by the given label.
Use the function observation to write a function endpoint that takes four arguments. The first three arguments are identical to the arguments passed to the function observation. The fourth argument is a string containing directions. The label provides a starting point on the map. The function must return the label of the end point on the map that is reached when the given route is followed completely. If it is not possible to follow the given route completely from the given starting point, the function must return the value None.
Use the function endpoint to write a function beehives that takes three arguments. The first two arguments are identical to the corresponding arguments passed to the functions observation and endpoint. The third argument is a string containing directions. The function must return a list containing the labels that are possible end positions that can be reached if the given route is followed completely. The same label can appear at most once in this list, and the labels must be listed in lexicographical order.

Example

>>> coord2label(0, 0)
'A1'
>>> coord2label(1, 5)
'B6'
>>> coord2label(7, 4)
'H5'

>>> label2coord('A1')
(0, 0)
>>> label2coord('B6')
(1, 5)
>>> label2coord('H5')
(7, 4)

>>> observation(2, 'abaabcabaabc', 'A1')
'a'
>>> observation(2, 'abaabcabaabc', 'B6')
'c'

>>> endpoint(2, 'abaabcabaabc', 'A5', 'bLaLa')
'A3'
>>> endpoint(2, 'abcdeecdea', 'B4', 'eLdLcUb')
'A2'
>>> endpoint(2, 'abcdeecdea', 'A3', 'cRdUcLbLaDa')

>>> beehives(2, 'abaabcabaabc', 'bLaLa')
['A1', 'A3', 'B1', 'B3']
>>> beehives(2, 'abcdeecdea', 'eLdLcUb')
['A2']
>>> beehives(2, 'abcdeecdea', 'cRdUcLbLaDa')
[]

Note that the possible routes leading to the four possible end points of the first example of the function beehives are depicted graphically in the introduction of this assignment.

Below, we show a representation of the rectangular map for the second example, with the row and column labels as used by the biologists. Labels of the squares that belong to a possible route are shown in black, and labels that do not belong to a route in gray. Labels that are possible a starting points of route are shown in blue, labels that are possible end points are shown in yellow, and labels that may both be a starting and end point are shown in green. This representation is also used as feedback for the test cases of the function beehives for which your submitted source code produces the wrong answer.

  12345

A abcde
B ecdea

De grote honingspeurder (Indicator indicator) uit Afrika is verzot op bijenwas, maar is niet altijd in staat om op zijn eentje een bijenkorf binnen te dringen. Daarom heeft hij een uniek samenwerkingsverband gesmeed met de mens. De vogel trekt de aandacht van lokale honingjagers met zijn ratelend geroep, vliegt in de richting van een bijenkorf, houdt regelmatig halt en roept dan opnieuw. Wanneer ze de bijenkorf bereiken, breekt de jager die open, bedwelmt de bijen met rook, neemt de honing eruit en laat de was over voor de vogel.

Deze samenwerking bespaart de mens gemiddeld 5,7 uur van de tijd om bijenkorven te zoeken, maar ze is niet onfeilbaar. "De grote honingspeurder heeft ons al naar de rand van een afgerond gebracht en tot bij een mannetjesolifant", rapporteren de biologen Lester Kort en Jennifer Horne. "In die gevallen waren er bijenkorven onderaan de klif (in een vallei) en achter de olifant. Zorg voor het welzijn van de begeleide personen behoort nu eenmaal niet tot het woordenboek van de honingspeurder."

Opgave

Een groep biologen is in de Keniaanse savanne bijenkorven in kaart aan het brengen. Hierbij laten ze zich leiden door de lokroep van de grote honingspeurder. Als ze zich tot bij een bijenkorf hebben laten leiden, dan duiden ze de locatie van de korf aan op een rechthoekige kaart. De kaart is onderverdeeld in vierkante gebieden. Zoals aangegeven in onderstaand voorbeeld zijn de rijen van de kaart van boven naar onder gelabeld met de hoofdletters A, B, …, en de kolommen van links naar rechts met de getallen 1, 2, 3, …. De vierkante gebieden zijn gelabeld met kleine letters die de soorten vegetatie aanduiden als herkenningspunten in de savanne.

Als de biologen met hulp van de honingspeurder een bijenkorf gevonden hebben, dan hebben ze geen enkel idee van de positie op de kaart waar ze vertrokken zijn. Gelukkig hebben ze een goed gevoel voor oriëntatie en kunnen ze de route die ze hebben afgelegd reconstrueren als een reeks opeenvolgende waarnemingen en bewegingen.

Een routebeschrijving kan omschreven worden als een string, waarin waarnemingen worden aangeduid met kleine letters die het soort vegetatie omschrijven en bewegingen met hoofdletters die de richting aangeven: L voor links, R voor rechts, O voor op en N voor neer. In een routebeschrijving wisselen waarnemingen en bewegingen elkaar steeds af, en de beschrijving begint en eindigt altijd met een waarneming. Indien het uitvoeren van een beweging zou leiden naar een vierkant buiten de kaart, dan wordt de beweging niet uitgevoerd en blijft men gewoon staan.

Je opdracht bestaat erin om voor een gegeven routebeschrijving alle mogelijke posities op de kaart te vinden waar de route kan eindigen. Deze geven de mogelijke posities van de bijenkorven aan. Stel dat we in bovenstaande kaart alle posities moeten vinden waar men kan eindigen als men de route bLaLa volgt. De mogelijke eindposities en de bijhorende routes worden aangegeven in onderstaande figuur.

In kolommen 2 en 5 staat er telkens een kleine letter b, en daar kan de route dus starten. Als we vanaf deze startposities naar links bewegen, dan komen we telkens op een vierkant terecht dat gelabeld is met de kleine letter a. We kunnen dus in alle gevallen de route verder blijven volgen. Als we nu opnieuw naar links bewegen, dan eindigen de routes die vertrokken zijn van kolom 5 op een vierkant in kolom 3. Daar staat telkens een kleine letter a, waardoor we de route volledig hebben kunnen volgen. De vierkanten in kolom 3 zijn daardoor mogelijke eindposities. De routes die vertrokken zijn vanaf kolom 2 eindigen na één beweging in kolom 1. Als we van daaruit terug naar links zouden bewegen, dan vallen we van de kaart. We blijven dus staan, maar eindigen zo terug op een vierkant met de kleine letter a. Ook in die gevallen hebben we dus de route volledig kunnen volgen, en zijn de vierkanten in kolom 1 mogelijke eindposities.

De positie van een vierkant op de kaart wordt door de biologen aangeduid met een label (een string) dat bestaat uit het rijlabel gevolgd door het kolomlabel. In Python is het echter gebruikelijk om rijen en kolommen te indexeren met natuurlijke getallen. Hierbij worden de rijen genummerd van boven naar onder en de kolommen van links naar rechts, telkens vanaf nul. Schrijf daarom eerst de volgende twee functies:

Een functie coord2label die voor een gegeven rij- en kolomindex (twee afzonderlijke argumenten) het corresponderende label teruggeeft.
Een functie label2coord die voor een gegeven label de corresponderende rij- en kolomindex teruggeeft als een tuple.

Je mag er hierbij van uitgaan dat het aantal rijen op de kaart nooit groter wordt dan 26. Gebruik nu de voorgaande functies bij de implementatie van de volgende functies.

Schrijf een functie waarneming waaraan drie argumenten moeten doorgegeven worden: i) het aantal rijen van een rechthoekige kaart, ii) een string van kleine letters die de labels van de vierkanten op de kaart aangeven, als we de vierkanten doorlopen van links naar rechts en van boven naar onder, en iii) het label van een vierkant op de kaart. De functie moet de kleine letter teruggeven die op het vierkant van de kaart staat dat door het label wordt aangeduid.
Gebruik de functie waarneming om een functie eindpunt te schrijven waaraan vier argumenten moeten doorgegeven worden. De eerste drie argumenten zijn dezelfde als bij de functie waarneming. Het vierde argument is een string die een routebeschrijving bevat. Het label geeft een startpunt aan op de kaart. De functie moet het label van het eindpunt op de kaart aangeven dat bereikt wordt als men de gegeven route volledig volgt. Indien het niet mogelijk is om vanaf het gegeven startpunt de gegeven route volledig te volgen, dan moet de functie de waarde None teruggeven.
Gebruik de functie eindpunt om een functie bijenkorven te schrijven waaraan drie argumenten moeten doorgegeven worden. De eerste twee argumenten zijn dezelfde als bij de functies waarneming en eindpunt. Het derde argument is een string die een routebeschrijving bevat. De functie moet een lijst teruggeven met de labels van alle mogelijke eindposities die men kan bereiken als de gegeven route gevolgd wordt. Hetzelfde label mag hoogstens één keer in deze lijst voorkomen, en de labels moeten in lexicografische volgorde voorkomen in de lijst.

Voorbeeld

>>> coord2label(0, 0)
'A1'
>>> coord2label(1, 5)
'B6'
>>> coord2label(7, 4)
'H5'

>>> label2coord('A1')
(0, 0)
>>> label2coord('B6')
(1, 5)
>>> label2coord('H5')
(7, 4)

>>> waarneming(2, 'abaabcabaabc', 'A1')
'a'
>>> waarneming(2, 'abaabcabaabc', 'B6')
'c'

>>> eindpunt(2, 'abaabcabaabc', 'A5', 'bLaLa')
'A3'
>>> eindpunt(2, 'abcdeecdea', 'B4', 'eLdLcOb')
'A2'
>>> eindpunt(2, 'abcdeecdea', 'A3', 'cRdOcLbLaNa')

>>> bijenkorven(2, 'abaabcabaabc', 'bLaLa')
['A1', 'A3', 'B1', 'B3']
>>> bijenkorven(2, 'abcdeecdea', 'eLdLcOb')
['A2']
>>> bijenkorven(2, 'abcdeecdea', 'cRdOcLbLaNa')
[]

We merken hierbij op dat de mogelijke routes die leiden naar de vier mogelijke eindpunten van het eerste voorbeeld van de functie bijenkorven grafisch worden weergegeven in de tekst hierboven.

Voor het tweede voorbeeld geven we hieronder een weergave van de rechthoekige kaart met de rij- en kolomlabels zoals ze door de biologen gebruikt worden. De labels van de vierkanten die tot een mogelijke route behoren hebben we weergegeven in het zwart, de labels die niet tot een route behoren in het grijs. De labels die een startpunt vormen van een mogelijke route staan in het blauw, de labels die een eindpunt vormen in het geel, en de labels die zowel startpunt als eindpunt zijn, staan in het groen. Deze voorstelling wordt ook gebruikt als feedback voor de testgevallen die een verkeerd antwoord geven voor de functie bijenkorven.

  12345

A abcde
B ecdea

Submit solution!

Added by:	Peter Dawyndt
Date:	2014-06-09
Time limit:	10s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	PY_NBC
Resource:	None

Informatics 1

PROG0482 - Feathered friends

Assignment

Example

Opgave

Voorbeeld