| Submit | All submissions | Best solutions | Back to list |
PROG0461 - Darts |
History
Darts is an age-old game that originates among soldiers who started competitions as a pastime between battles. They threw short arrows at the bottom of wine barrels and later at discs made of the trunks of trees. Scores were added onto the discs. Out of necessity, the sport was played inside during the winter months, which forced the soldiers to replace the arrows with darts and led to a new set of rules for practicing the indoor sport. As the game continued to develop, the richer layers of population gained an interest in darts. It is written that Hendrik VIII's second wife Anne Boleyn gave him a richly decorated Biscayan darts set.
Dartboard
The current game board comes from London. The board consists of a round fiber plate of 18 millimetres thick, on which sisal fiber bristles are glued and pressed under large pressure. The whole is framed by a metal band. The board is provided with a section division using different colours. After that, a metal web is fixed on top of the plate, provided with the same division. The function of this web is to make sure it is always clear in which section the dart landed. On the outer border, a metal ring is placed on which numbers are fixed according to the section division. This ring can be unlinked from the rest of the board, making it possible to shift the numbers with regard to the plate.
The idea is that the section (bed) 20 is in the middle on top. This section is usually the most thrown on. This is why the bottom plate of this section is likely to break first. Every dart that is thrown affects the fibers of the board. The glue layer prevents the board from falling apart, but after a while, an accumulation of fibers will be visible under the form of lumps. To prevent this, the board should be turned around as much as possible, so that 20 is always on top of another section. Do note that 20 should always be on top of a black section. Modern sisal fiber boards shouldn't be made wet (unlike what is often thought).
The measurements of a dartboard are indicated in the picture above. The double ring and triple ring are always 9.6 mm wide.
Scoring
The dartboard is divided in rings and sections. The numbers at the rim indicate the amount of points you receive for throwing a dart in that particular section. The sections are subdivided in a number of smaller partitions.
- in the middle is the double bull or bull's eye (red), 50 points
- around the double bull is the single bull (green), 25 points
- around that a wide ring, the bed (black and white), for which the amount of points that is indicated on the rim of the board is granted
- around that a smaller ring, the triple (or treble) ring (red and green); this yields a triple score of the bed
- around that is another bed
- around that is the double ring (red en green) yields a double score of the bed
If you throw a dart in the outer black rim (where the numbers are) or next to the board, you don't get any points. A bouncer, which is a dart that bounces back from the board, doesn't get a score. You also won't receive any points if one of your darts falls out of the board before you were able to take your darts out (please note, officially this isn't called a bouncer). If a player throws in one of his formerly thrown darts (a 'Robin Hood'), the last dart doesn't receive a score.
Assignment
We consider a Cartesian co-ordinate scale with its origin in the centre of the bull's eye of a dartboard. A player throws a dart to the board that lands on co-ordinates $(x, y)$, the co-ordinates are expressed in millimetres. Determine the score that is obtained by this dart. Work as follows:
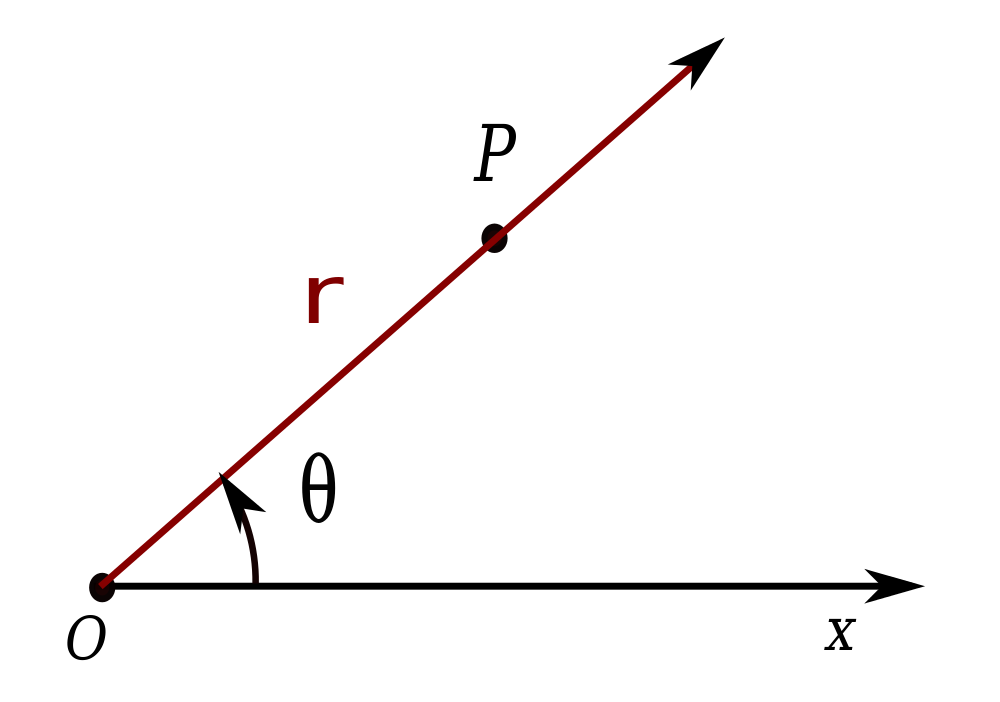
- Write a function polar to which two real numbers $x$ and $y$ must be given. These numbers represent the position $(x, y)$ of a point $P$ in the Cartesian co-ordinates scale. The function must print a tuple $(r, \theta)$ of real numbers, that expresses the position of a point $P$ in polar co-ordinates, where the pole $O$ coincides with the centre of the bull's eye, and the pole axis coincides with the $X$ axis. The co-ordinate $r$ of the point $P$ is the distance $OP$. The co-ordinate $\theta$ indicates the oriented angle between the positive $X$ axis and the half straight line of O through P. This angle is expressed in radians, and $-\pi < \theta \leq \pi$ must apply. The connection between the Cartesian co-ordinates $(x, y)$ and the pole co-ordinates $(r, \theta)$ is than given by $$\begin{cases} r = & \sqrt{x^2+y^2} \\ \\ \theta = & \arctan\left(\frac{y}{x}\right) \end{cases}$$
- Use the function polar to write a function darts, to which two integers $x$ and $y$ must be given. These numbers represent the position $(x, y)$ of a point $P$ in the Cartesian co-ordinates scale, and are expressed in millimetres. As a third, optional argument scores, a sequence (or a list or tuple) of integers can be given to this function. The amount of numbers in the sequence determines the number of sectors in which the dartboard is divided. The numbers indicate the scoring if the sectors are run through clockwise, starting with the section that contains the points on the positive $Y$ axis. This last sector is always situated symmetrically with regard to the positive $Y$ axis. If no explicit score was given to the function, use the score 1, 2, …, 20. The function must print the score that is obtained if a dart that is thrown at the board and lands on the position $(x, y)$ in the Cartesian co-ordinate scale with its origin in the centre of the bull's eye.
From angle to sector
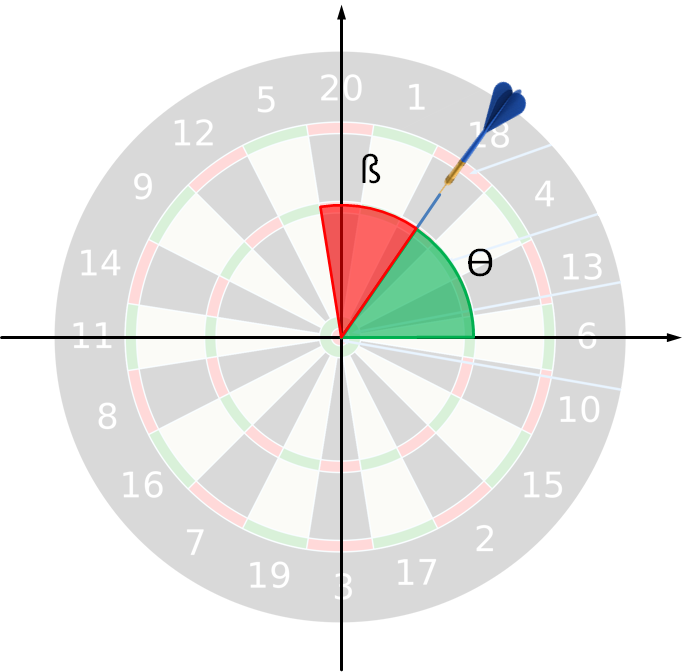
One of the difficulties of this exercise is how to determine the sector on the board in which the dart is thrown. The sketch given below illustrates how an angle in polar coordinates ($\theta$; the green angle) can be converted into an angle ($\beta$; the red angle) that can be used to determine the corresponding sector.
Using a little bit of trigonometry, it is easy to see that $$ \beta + \theta = \frac{\pi}{2} + \frac{\pi}{s}\,, $$ where $s$ represents the number of sectors. In other words, $$ \beta = \frac{\pi}{2} + \frac{\pi}{s} - \theta\,. $$ Once $\beta$ has been computed and you know that each sector covers an angle of $\frac{2\pi}{s}$, you can convert the angle $\beta$ into the index of the sector. The first sector (the one on top of the $Y$-axis) has index 0, the one to the right of it has index 1, and so on in a clockwise manner.
Example
>>> polar(137, 0) (137.0, 0.0) >>> polar(104.5, 0) (104.5, 0.0) >>> polar(0, 200) (200.0, 1.5707963267948966) >>> polar(0, 166.3) (166.3, 1.5707963267948966) >>> polar(-30.0, 22.0) (37.20215047547655, 2.5088438185876103) >>> darts(137, 0) 6 >>> darts(104.5, 0) 18 >>> darts(0, 200) 0 >>> darts(0, 166.3) 2 >>> darts(-30.0, 22.0) 18 >>> points = [20, 1, 18, 4, 13, 6, 10, 15, 2, 17, 3, 19, 7, 16, 8, 11, 14, 9, 12, 5] >>> darts(137, 0, scores=points) 6 >>> darts(104.5, 0, scores=points) 18 >>> darts(0, 200, scores=points) 0 >>> darts(0, 166.3, scores=points) 40 >>> darts(-30.0, 22.0, scores=points) 9
Geschiedenis
Darts (of darten) is een eeuwenoud spel dat zou ontstaan zijn toen soldaten wedstrijden begonnen te houden als tijdverdrijf tussen veldslagen door. Daarbij werden korte speren gegooid op omgekeerde bodems van wijntonnen en later op doorgezaagde boomstamschijven. Op de schijven werd een puntentelling aangebracht. In de wintermaanden werd de sport noodgedwongen binnen gehouden, wat tot gevolg had dat men de kleine speren moest vervangen door darts en er een nieuwe regelgeving voor het beoefenen van de binnensport werd bedacht. Naarmate het spel zich verder ontwikkelde, begonnen de rijkere lagen van de bevolking ook interesse te tonen in darts. Zo staat er geschreven dat Hendrik VIII in 1530 van zijn tweede vrouw Anne Boleyn een kostbaar versierde Biscayan-dartset geschonken kreeg.
Een oude Nederlandse en in de Vlaamse spreektaal nog gebruikelijke naam van het spel is vogelpik. Deze term is afkomstig van een soortgelijk spel dat vroeger gespeeld werd in cafés. Dit spel bestond uit een roos met ringen, niet zoals het actueel dartbord dus, en een nagemaakte vogel met een scherpe snavel. De vogel werd met een koord aan het plafond opgehangen en de spelers probeerden de snavel van de vogel in de roos te zwieren.
Dartbord
Het wedstrijdbord dat tegenwoordig gebruikt wordt komt uit Londen. Het bord bestaat uit een ronde vezelplaat van 18 millimeter dik, waarop sisalvezelborsteltjes onder grote druk gelijmd en geperst worden. Het geheel wordt omlijst door een metalen band. Het bord wordt voorzien van een vakindeling door middel van verschillende kleuren. Vervolgens wordt er een metalen web op bevestigd dat diezelfde vakindeling heeft. De functie van dit web is er voor te zorgen dat altijd duidelijk is in welk vak een dart gegooid is. Op de buitenzijde wordt een metalen ring aangebracht waarop volgens de vakindeling bepaalde cijfers zijn bevestigd. Deze ring is los te maken, zodat de cijfers ten opzichte van het bord verschoven kunnen worden.
Het is de bedoeling dat het vak (bed) 20 middenboven zit. Op deze 20 wordt normaal gesproken het meest gegooid. Hierdoor zal de bodemplaat in dit vak dan ook het eerste kapot gaan. Elke dart die gegooid wordt tast de vezeltjes van het bord aan. Door de lijmlaag valt het bord niet uit elkaar, maar na verloop van tijd wordt op bepaalde plaatsen een opeenhoping van vezeltjes zichtbaar, in de vorm van bulten. Om dit te voorkomen dient het bord om de zoveel tijd gedraaid te worden, zodat het cijfer twintig weer boven een nieuw, minder gehavend deel van het bord staat. De 20 staat wel altijd boven een zwart deel. Moderne sisalvezelborden moeten beslist niet worden natgemaakt zoals nog wel wordt gedacht.
De afmetingen van het dartbord worden aangegeven in bovenstaande figuur. De double ring en triple ring zijn telkens 9.6 mm breed.
Puntentelling
Het dartbord is verdeeld in ringen en sectoren. De getallen langs de rand geven het aantal punten aan voor een pijltje in de desbetreffende sector. Deze sectoren zijn onderverdeeld in nog een aantal kleinere vakken.
- in het midden is de double bull of bull's eye (rood), 50 punten
- daaromheen de single bull (groen), 25 punten
- daaromheen een brede ring, het bed (zwart en wit), waarvoor het aantal punten geldt dat op de rand van het bord staat
- daaromheen een smalle ring, de triple (of treble) ring (rood en groen); deze levert drie maal het puntenaantal op
- daaromheen weer een bed
- daaromheen de double ring (rood en groen) met twee keer het aantal punten dat bij het betreffende vak staat
Een dart in de buitenste zwarte rand (waar de cijfers staan) of naast het bord levert geen punten op. Een bouncer, een dart die van het bord terugkaatst, heeft geen score tot gevolg. Daarnaast is er ook geen score wanneer een dart na geworpen te zijn plots uit het bord valt voordat de speler in de gelegenheid was alle 3 zijn pijlen uit het bord te halen (let wel, dit wordt officieel geen bouncer genoemd). Als een speler een dart in één van zijn eerder gegooide darts gooit (een 'Robin Hood'), wordt de laatste van die twee darts wel gezien als zijnde 'geworpen', maar wordt er geen score aan die dart toegekend.
Opgave
We beschouwen een carthesisch coördinatenstelsel met oorsprong in het centrum van de bull's eye van een dartboard. Een speler werpt een pijltje naar het dartbord dat belandt op de coördinaten $(x, y)$, waarbij beide coördinaten worden uitgedrukt in millimeter. Bepaal het aantal punten dat met dit pijltje behaald wordt. Hiervoor ga je als volgt te werk:
- Schrijf een functie poolcoordinaten waaraan twee reële getallen $x$ en $y$ moeten doorgegeven worden. Deze getallen stellen de positie $(x, y)$ van een punt $P$ in het carthesisch coördinatenstelsel voor. De functie moet een tuple $(r, \theta)$ van reële getallen teruggeven, dat de positie van het punt $P$ uitdrukt in poolcoördinaten, waarbij de pool $O$ samenvalt met het centrum van de bull's eye, en de poolas samenvalt met de $X$-as. De coördinaat $r$ van het punt $P$ is de afstand $OP$. De coördinaat $\theta$ geeft de georiënteerde hoek aan tussen de positieve $X$-as en de halfrechte van O door P. Deze hoek wordt uitgedrukt in radialen, en er moet gelden dat $-\pi < \theta \leq \pi$. Het verband tussen de carthesische coördinaten $(x, y)$ en de poolcoördinaten $(r, \theta)$ wordt dan gegeven door $$\begin{cases} r = & \sqrt{x^2+y^2} \\ \\ \theta = & \arctan\left(\frac{y}{x}\right) \end{cases}$$
- Gebruik de functie poolcoordinaten om een functie darts te schrijven, waaraan twee reële getallen $x$ en $y$ moeten doorgegeven worden. Deze getallen stellen de positie $(x, y)$ van een punt $P$ in het carthesisch coördinatenstelsel voor, en worden uitgedrukt in millimeter. Als derde argument scores kan aan de functie optioneel ook nog een reeks (een lijst of een tuple) van natuurlijke getallen doorgegeven worden. Het aantal getallen in de reeks bepaalt het aantal sectoren waarin het dartbord verdeeld wordt. De getallen geven de puntentelling aan wanneer de sectoren in wijzerzin worden doorlopen, te beginnen bij de sector die de punten op de positieve $Y$-as bevat. Deze laatste sector bevindt zich altijd symmetrisch ten opzichte van de positieve $Y$-as. Indien geen expliciete puntenreeks wordt doorgegeven aan de functie, dan moet de puntenreeks 1, 2, …, 20 gebruikt worden. De functie moet het aantal punten teruggeven dat behaald wordt als een pijltje naar het bord geworpen wordt, dat belandt op positie $(x, y)$ in het carthesisch coördinatenstelsel met oorsprong in het centrum van de bull's eye.
Van hoek naar sector
Een van de moeilijkheden bij deze opgave is het bepalen van de sector op het bord waarin het pijltje geworpen wordt. Onderstaande schets maakt duidelijk hoe je een hoek in poolcoördinaten ($\theta$; de groene hoek) kunt omzetten naar een hoek ($\beta$; de rode hoek) die je kunt gebruiken om de overeenkomstige sector te bepalen.
Met een beetje goniometrie is het makkelijk in te zien dat $$ \beta + \theta = \frac{\pi}{2} + \frac{\pi}{s}\,, $$ waarbij $s$ het aantal sectoren voorstelt. Met andere woorden $$ \beta = \frac{\pi}{2} + \frac{\pi}{s} - \theta\,. $$ Als je eenmaal $\beta$ bepaald hebt, en je weet dat elke sector een hoek van $\frac{2\pi}{s}$ beslaat, dan kan je de hoek $\beta$ omzetten naar de index van de sector. De eerste sector (deze bovenaan de $Y$-as) heeft dan index 0, die rechts ervan index 1, enzoverder in wijzerzin.
Voorbeeld
>>> poolcoordinaten(137, 0) (137.0, 0.0) >>> poolcoordinaten(104.5, 0) (104.5, 0.0) >>> poolcoordinaten(0, 200) (200.0, 1.5707963267948966) >>> poolcoordinaten(0, 166.3) (166.3, 1.5707963267948966) >>> poolcoordinaten(-30.0, 22.0) (37.20215047547655, 2.5088438185876103) >>> darts(137, 0) 6 >>> darts(104.5, 0) 18 >>> darts(0, 200) 0 >>> darts(0, 166.3) 2 >>> darts(-30.0, 22.0) 18 >>> punten = [20, 1, 18, 4, 13, 6, 10, 15, 2, 17, 3, 19, 7, 16, 8, 11, 14, 9, 12, 5] >>> darts(137, 0, scores=punten) 6 >>> darts(104.5, 0, scores=punten) 18 >>> darts(0, 200, scores=punten) 0 >>> darts(0, 166.3, scores=punten) 40 >>> darts(-30.0, 22.0, scores=punten) 9
| Added by: | Peter Dawyndt |
| Date: | 2014-03-31 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |


 RSS
RSS