| Submit | All submissions | Best solutions | Back to list |
PROG0425 - Eye of Horus |
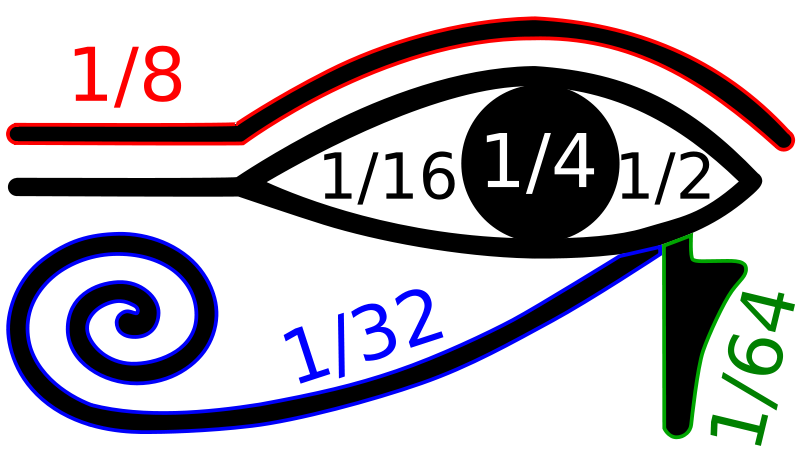
The Eye of Horus is an ancient Egyptian symbol of protection, royal power and good health. The eye is personified in the goddess Wadjet. Different parts of the Eye of Horus were thought to be used by the ancient Egyptians to represent one divided by the first six powers of two, as shown in the image below.
An Egyptian fraction is the sum of distinct unit fractions, such as $\frac{1}{2} + \frac{1}{3} + \frac{1}{16}$. That is, each fraction in the expression has a numerator equal to 1 and a denominator that is a positive integer, and all the denominators differ from each other. The value of an expression of this type is a positive rational number $\frac{a}{b}$. For instance, the Egyptian fraction above sums to $\frac{43}{48}$. It has been proven that every positive rational number can be represented by an Egyptian fraction.
Sums of this type were used as a serious notation for rational numbers by the ancient Egyptians, and continued to be used by other civilizations into medieval times. The Rhind Papyrus of 500 BC already mentions these Egyptian fractions as an "ancient method" and they are thought to date back to the time of the early pyramids. Leonardo de Pisa's famous book Liber Abaci of 1215 AD — which introduced the concept of zero to European mathematicians, the Hindu-Arabic system of numeration, and the famous rabbit sequence (Leonardo's nickname was Fibonacci) — also describes this kind of fraction decomposition. In modern mathematical notation, Egyptian fractions have been superseded by vulgar fractions and decimal notation.
An easy way to write a given fraction as an Egyptian fraction is to repeatedly take the largest unit fraction that will fit, subtract to find what remains, and repeat until the remainder is a unit fraction. For instance, 7 divided by 15 is less than $\frac{1}{2}$ but more than $\frac{1}{3}$, so the first unit fraction is $\frac{1}{3}$ and the first remainder is $\frac{2}{15}$. Then $\frac{2}{15}$ is less than $\frac{1}{7}$ but more than $\frac{1}{8}$, so the second unit fraction is $\frac{1}{8}$ and the second remainder is $\frac{1}{120}$. The latter fraction is itself a unit fraction, so we are finished: $$\frac{7}{15} = \frac{1}{3} + \frac{1}{8} + \frac{1}{120}$$ During these computations we always use the irreducible version of a fraction $\frac{a}{b}$. A fraction is said to be irreducible if its numerator $a$ and denominator $b$ are coprime. A reducible fraction can be converted into an equivalent irreducible fraction by dividing both the numerator and the denominator by the greatest common divisor (gcd) of both integers. The gcd of two integers can be computed using the gcd function from the fractions module in the Python Standard Library.
>>> from fractions import gcd >>> gcd(20, 8) 4
There are other algorithms for decomposing a given fraction than an Egyptian fraction, but there is no algorithm that guarantees a maximum number of terms or a minimum largest denominator. For instance, the greedy algorithm described above leads to $$\frac{5}{121} = \frac{1}{25} + \frac{1}{757} + \frac{1}{763309} + \frac{1}{873960180913} + \frac{1}{1527612795642093418846225}$$ but a simpler rendering of the same number is $$\frac{5}{121} = \frac{1}{33} + \frac{1}{121} + \frac{1}{363}$$
Remark
For this exercise you have to make sure that you compute with fractions having integer numerators and denominators. As soon as you start working with floating point numbers to perform computations based on the decimal representation of the fractions, you will get into trouble because of rounding errors in the representation of floats.
Input
A fraction $\frac{a}{b}$, where the numerator $a \in \mathbb{N_0}$ and the denominator $b \in \mathbb{N_0}$ are on two separate lines. You may assume that $0 < \frac{a}{b} \leq 1$.
Output
The list of denominators of the decomposition of the fraction $\frac{a}{b}$ as an Egyptian fraction, using the greedy method described above. The denominators should be listed in increasing order, each on a separate line.
Example
Input:
47 60
Output:
2 4 30
Example
Input:
7 15
Output:
3 8 120
Example
Input:
5 41
Output:
9 93 11439
Het Oog van Horus — het alziende oog — werd in het oude Egypte gebruikt als symbool voor bescherming, goddelijke kracht en goede gezondheid. Het oog wordt verpersoonlijkt in de vrouwelijke zonnegodin Wadjet. De afzonderlijke onderdelen van het oog staan voor ruiken, zien, denken, horen, proeven en voelen. Men gaat ervan uit dat de oude Egyptenaren deze onderdelen gebruikten als voorstelling voor één gedeeld door de eerste zes machten van twee, zoals aangegeven in onderstaande figuur.
Een Egyptische breuk is een som van verschillende eenheidsbreuken, zoals $\frac{1}{2} + \frac{1}{3} + \frac{1}{16}$. Daarbij heeft elke breuk in de uitdrukking een teller die gelijk is aan 1 en een natuurlijk getal als noemer. Alle breuken hebben bovendien een verschillende noemer. De waarde van een dergelijke uitdrukking is een positief rationaal getal $\frac{a}{b}$. Zo sommeert bovenstaande Egyptische breuk bijvoorbeeld tot $\frac{43}{48}$. Het is bewezen dat elk positief rationaal getal kan geschreven worden als een Egyptische breuk.
De oude Egyptenaren gebruikten sommen van dit type om rationale getallen te noteren, en verschillende andere volkeren bleven ze gebruiken tot laat in de middeleeuwen. De Rhind-papyrus uit 500 voor Christus maakt reeds melding van Egyptische breuken als een "oude methode" en er wordt gedacht dat ze teruggaan tot de tijd van de allereerste piramiden. Het bekende boek Liber Abaci van Leonardo de Pisa uit 1215 na Christus — dat Europese wiskundigen concepten bijbracht zoals het getal nul, het Hindu-Arabische talstelsel, en de wereldberoemde konijnenrij (Fibonacci was het pseudoniem van Leonardo) — beschrijft ook hoe breuken op deze manier kunnen ontbonden worden. In de moderne wiskunde hebben Egyptische breuken plaats moeten ruimen voor gewone breuken en de decimale voorstelling van rationale getallen.
Een eenvoudige manier om een gegeven breuk te schrijven als een Egyptische breuk bestaat erin om telkens de grootste eenheidsbreuk te nemen die nog in de breuk past, deze van de breuk af te trekken om te berekenen wat nog rest, en dit te blijven herhalen totdat de resterende breuk een eenheidsbreuk is. Aangezien bijvoorbeeld 7 gedeeld door 15 kleiner is dan $\frac{1}{2}$ maar groter is dan $\frac{1}{3}$, is de eerste eenheidsbreuk gelijk aan $\frac{1}{3}$ en is de eerste rest gelijk aan $\frac{2}{15}$. Daarna volgt dat $\frac{2}{15}$ kleiner is dan $\frac{1}{7}$ maar groter dan $\frac{1}{8}$, waardoor de tweede eenheidbreuk gelijk is aan $\frac{1}{8}$ en de tweede rest gelijk aan $\frac{1}{120}$. Deze laatste breuk is zelf een eenheidsbreuk, waardoor we klaar zijn met de ontbinding: $$\frac{7}{15} = \frac{1}{3} + \frac{1}{8} + \frac{1}{120}$$ Tijdens deze berekeningen maken we steeds gebruik van de meest vereenvoudigde vorm van een breuk $\frac{a}{b}$. Een breuk is in zijn meest vereenvoudigde vorm als de teller $a$ en noemer $b$ geen gemeenschappelijke delers hebben. De meest vereenvoudigde vorm kan dus gevonden worden door teller en noemer te delen door de grootste gemeenschappelijke deler (ggd) van beide getallen.
De ggd van twee natuurlijke getallen kan berekend worden aan de hand van de gcd functie uit de fractions module van de Python Standard Library.
>>> from fractions import gcd >>> gcd(20, 8) 4
Er bestaan nog andere algoritmen om een gegeven breuk als een Egyptische breuk te ontbinden, maar er bestaat geen algoritme dat altijd een grootste aantal termen of een kleinst mogelijke noemer garandeert. Zo resulteert het gretige algoritme dat hierboven werd beschreven bijvoorbeeld in $$\frac{5}{121} = \frac{1}{25} + \frac{1}{757} + \frac{1}{763309} + \frac{1}{873960180913} + \frac{1}{1527612795642093418846225}$$ terwijl er een eenvoudigere ontbinding van dezelfde breuk bestaat onder de vorm $$\frac{5}{121} = \frac{1}{33} + \frac{1}{121} + \frac{1}{363}$$
Opmerking
Zorg ervoor dat je in deze opgave rekent met breukvormen, waarbij de teller en de noemer beide gehele getallen vormen. Als je gaat werken met floating point getallen om te rekenen met een decimale voorstelling van de breuken, dan zal je in de problemen raken omwille van de afrondingsfouten die hierbij optreden.
Invoer
Een breuk $\frac{a}{b}$, waarbij de teller $a \in \mathbb{N_0}$ en de noemer $b \in \mathbb{N_0}$ elk op een afzonderlijke regel staan. Je mag ervan uitgaan dat $0 < \frac{a}{b} \leq 1$.
Uitvoer
De lijst van noemers van de ontbinding van de breuk $\frac{a}{b}$ als een Egyptische breuk, die resulteert als het gretige algoritme wordt toegepast dat hierboven werd beschreven. De noemers moeten van klein naar groot opgelijst worden, elk op een afzonderlijke regel.
Voorbeeld
Invoer:
47 60
Uitvoer:
2 4 30
Voorbeeld
Invoer:
7 15
Uitvoer:
3 8 120
Voorbeeld
Invoer:
5 41
Uitvoer:
9 93 11439
| Added by: | Peter Dawyndt |
| Date: | 2013-09-11 |
| Time limit: | 30s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS