| Submit | All submissions | Best solutions | Back to list |
PROG0412 - Election posters |
A billboard is divided into vertical strips that are all of the same width. A series of posters are successively attached to the board. The posters have the same height as the billboard itself, are attached at different positions on the billboard, and thereby exactly cover a sequence of strips. However, the poster are not all of the same width, and are possibly stuck on top of each other. How many posters will finally be (partially) visible.
As an example, suppose that a billboard has ten strips and five posters are attached to it in the following order:
- a poster that starts at strip 1 and is 4 strips wide
- a poster that starts at strip 2 and is 5 strips wide
- a poster that starts at strip 8 and is 3 strips wide
- a poster that starts at strip 3 and is 2 strips wide
- a poster that starts at strip 7 and is 4 strips wide
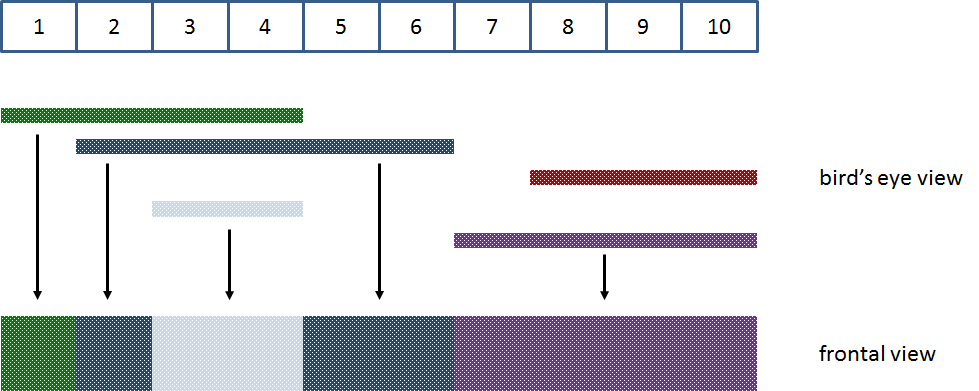
A graphical representation of this situation as given below, clearly shows that in the end four out of five posters are (partially) visible.
Note that you should not make the assumption that billboards are always subdivided into ten strips, as is the case in the above example.
Assignment
Write a function visible that takes a list of tuples, where each tuple contains two integers. The tuples describe the positions and the order of a sequence of posters that are attached on a billboard. The first tuple corresponds to the poster that is attached first. The last tuple with the poster that is attached at the end. The first integer of a tuple gives the index of the strip that is covered by the left part of the poster, and the second integer indicates the number of strips covered by the poster. The function should return how many posters are eventually (partially) visible.
Example
>>> visible([(1, 4), (2, 5), (8, 3), (3, 2), (7, 4)]) 4 >>> visible([(3, 5), (1, 4), (5, 6)]) 2 >>> visible([(2, 1), (5, 1)]) 2
Een aanplakbord wordt verdeeld in verticale stroken die allemaal even breed zijn. Op het bord worden achtereenvolgens een aantal verkiezingsposters geplakt. De posters zijn even hoog als het bord zelf, worden op verschillende plaatsen aangebracht, en bedekken daarbij precies een aantal opeenvolgende stroken. De posters zijn evenwel niet allemaal even breed, en worden mogelijks over elkaar heen geplakt. Vraag is hoeveel posters er finaal nog voor minstens een deel zichtbaar zijn.
Veronderstel bijvoorbeeld dat een aanplakbord tien stroken heeft, en dat er achtereenvolgens vijf posters op geplakt worden:
- een poster die begint vanaf strook 1 en 4 stroken breed is
- een poster die begint vanaf strook 2 en 5 stroken breed is
- een poster die begint vanaf strook 8 en 3 stroken breed is
- een poster die begint vanaf strook 3 en 2 stroken breed is
- een poster die begint vanaf strook 7 en 4 stroken breed is
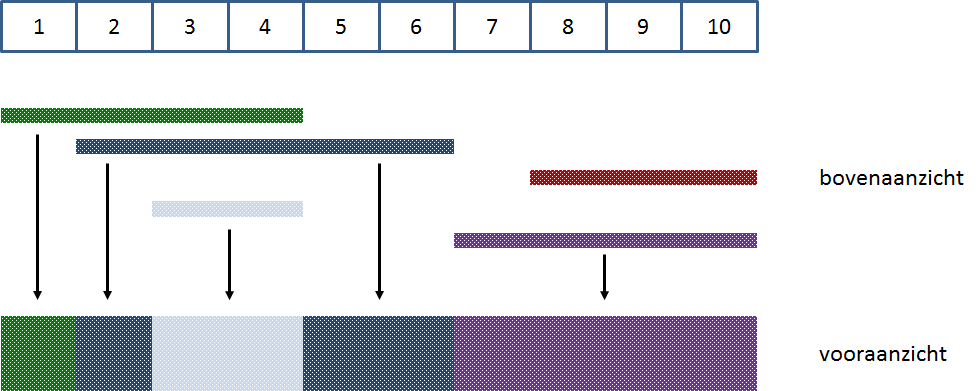
Uit onderstaande grafische voorstelling van deze situatie blijkt dat er uiteindelijk nog vier van de vijf posters (gedeeltelijk) zichtbaar zijn.
Merk op dat je er niet a priori mag van uitgaan dat aanplakborden altijd onderverdeeld zijn in tien stroken, zoals dat het geval is in bovenstaand voorbeeld.
Opgave
Schrijf een functie zichtbaar waaraan een lijst van tuples moet doorgegeven worden, waarbij elk tuple twee natuurlijke getallen bevat. Deze tuples beschrijven de posities van een aantal posters die in de opgelijste volgorde op een aanplakbord aangebracht worden. Het eerste tuple komt dus overeen met de poster die eerst wordt aangebracht. Het laatste tuple met de poster die als laatste wordt aangebracht. Het eerste getal van een tuple geeft de strook aan waar het linkerdeel van de poster wordt aangebracht, en het tweede getal van een tuple geeft aan hoeveel stroken de poster breed is. De functie moet teruggeven hoeveel posters er uiteindelijk nog (gedeeltelijk) zichtbaar zijn.
Voorbeeld
>>> zichtbaar([(1, 4), (2, 5), (8, 3), (3, 2), (7, 4)]) 4 >>> zichtbaar([(3, 5), (1, 4), (5, 6)]) 2 >>> zichtbaar([(2, 1), (5, 1)]) 2
| Added by: | Peter Dawyndt |
| Date: | 2013-08-31 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS