| Submit | All submissions | Best solutions | Back to list |
PROG0408 - Cell towers |
A telephone company is putting down cell towers to further improve their mobile phone network. It wants to place the towers in such a way that the average signal strength over a range of reception points is as large as possible.
If a signal is sent from a tower with co-ordinates $(x_z, y_z)$, we assume in this assignment that the signal strength $s \in [0, 1]$ in a reception point with co-ordinates $(x_o, y_o)$ only depends on the distance $r$ between the reception point and the towers, and on a parameter $\alpha$ that indicates the power of the towers. The distance is given by $$r = \sqrt{(x_o - x_z)^2 + (y_o - y_z)^2}$$ We will also assume that all towers have the same amount of power. Each model can therefor be described by a signal function $f(r, \alpha)$. This function takes a value between 0 and 1 for a point on a given distance to the tower, which indicates the signal power level.
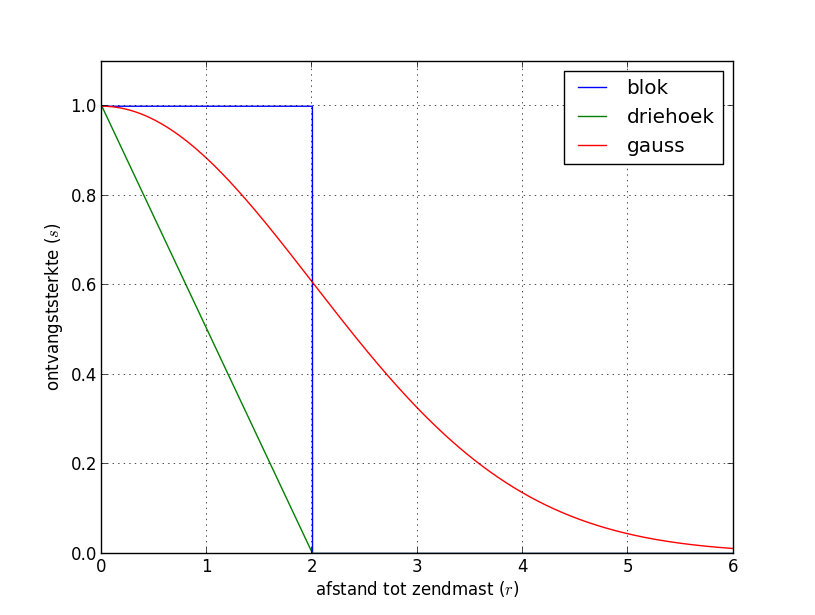
The graph above shows the course of the signal strength $s$ for a number of models, as a function of the distance $r$ to the tower:
- block strength (block): all points within a radius $\alpha$ (including the points on the edge) have signal power level 1, and the external points have signal power level 0
- triangular strength (triangle): the signal strength decreases linearly from 1 at the tower to 0 for points at a distance $\alpha$ to the tower; points at a distance larger than $\alpha$ to the tower also have signal power level 0
- strength according to Gaussian function (gauss): the signal strength is provided by $e^{\frac{-r^2}{2\alpha^2}}$
If a reception point receives signals from multiple towers, then the signal strength at that point equals the maximum signal strength of the signals from the individual towers.
Preparation
In Python functions are themselves objects, so you can use them like any other objects. In particular, you can assign functions to variables or pass them as an argument to other functions. For example, consider the following three functions.
def repeat(value, function, number): for i in range(number): value = function(value) return value def increase(value): return value + 1 def decrease(value): return value - 1
Below is an example of how these functions can be used. Check how Python reacts when you run the following sequence of instructions within an interactive Python session where you first ensure that the above functions were defined. Make sure that you understand why you get a certain value, and what actually happens in the interactive session before proceeding with the actual task.
>>> increase(5) >>> decrease(101) >>> repeat(5, increase, 3) >>> repeat(5, decrease, 3) >>> repeat(5, decrease, increase(3))
Assignment
- Write three functions block, triangle and gauss, that constitute an implementation of the corresponding signal functions described in the introduction of this assignment. Each function should be passed two arguments: a distance $r$ between a tower and a reception point, and the strength $\alpha$ of the tower. Each function should return the corresponding signal strength as a real number between 0 and 1.
- Write a function receptionquality that returns the average signal strength, measured over a series of reception points. The function has two obligatory parameters towers and receptionpoints to which respectively a list of co-ordinates of the towers and a list of co-ordinates of reception points must be passed. Each co-ordinate is then represented as a tuple $(x, y)$. The function also has two optional parameters. A parameter alpha, indicating the strength $\alpha$ of the towers (default value 5.0), and a parameter signalfunction to which a signal function $f(r, \alpha)$ can be passed that models the type of the towers (towers usually have a block strength.)
Example
>>> block(1.0, 2.0) 1.0 >>> triangle(1.0, 2.0) 0.5 >>> gauss(1.0, 2.0) 0.8824969025845955 >>> towers = [(0.0, 0.0), (5.0, 5.0), (3.0, 4.0)] >>> receptionpoints = [(1.2, 4.3), (2.8, 3.3), (3.2, 0.7), (-1.0, -1.0), (10.0, 0.0)] >>> receptionquality(towers, receptionpoints) 0.8 >>> receptionquality(towers, receptionpoints, alpha=3.0) 0.6 >>> receptionquality(towers, receptionpoints, signalfunction=triangle) 0.5102911527511019 >>> receptionquality(towers, receptionpoints, signalfunction=gauss) 0.8121116675748477
Below is a map that shows the situation for the first case in the above doctest. After you have submitted your solution, you can also view some maps to assist you in debugging. By clicking on the reception points of the towers you will see additional information.
Een telecommunicatiebedrijf wil bij het uitbouwen van een netwerk voor mobiele telefonie een aantal zendmasten neerplanten. Het wil de zendmasten op zo een manier plaatsen, dat de gemiddelde ontvangstkwaliteit over een reeks van ontvangstpunten zo groot mogelijk is.
Als een signaal wordt uitgezonden door een zendmast met coördinaten $(x_z, y_z)$, dan gaan we er voor deze opgave van uit dat de ontvangstkwaliteit $s \in [0, 1]$ in een ontvangstpunt met coördinaten $(x_o, y_o)$ enkel afhangt van de afstand $r$ tussen het ontvangstpunt en de zendmasten, en van een parameter $\alpha$ die de sterkte van de zendmasten aangeeft. Daarbij wordt de afstand gegeven door $$r = \sqrt{(x_o - x_z)^2 + (y_o - y_z)^2}$$ We gaan er voor de eenvoud ook van uit dat alle zendmasten eenzelfde sterkte hebben. Elk model van zendmast kan daardoor omschreven worden door een signaalfunctie $f(r, \alpha)$. Deze functie neemt voor een punt op een gegeven afstand tot de zendmast een waarde tussen 0 en 1 aan die de ontvangststerkte aangeeft.
Bovenstaande figuur toont het verloop van de ontvangststerkte $s$ voor een aantal modellen van zendmasten, in functie van de afstand $r$ tot de zendmast:
- blokvormige sterkte (blok): alle punten binnen straal $\alpha$ (inclusief de punten op de rand) hebben ontvangststerkte 1, en de punten daarbuiten hebben ontvangststerkte 0
- driehoeksvormige sterkte (driehoek): de ontvangststerkte neemt lineair af van 1 op het punt van de zendmast tot 0 voor punten op afstand $\alpha$ van de zendmast; punten met een afstand groter dan $\alpha$ tot de zendmast hebben ook ontvangststerkte 0
- sterkte volgens Gausscurve (gauss): de ontvangststerkte wordt gegeven door $e^{\frac{-r^2}{2\alpha^2}}$
Als een ontvangstpunt signalen ontvangt van meerdere zendmasten, dan is de ontvangststerkte op dat punt gelijk aan de maximale ontvangststerkte van de signalen van de individuele zendmasten.
Voorbereiding
In Python zijn functies zelf ook objecten, waardoor je ze kunt gebruiken zoals alle andere objecten. In het bijzonder kun je functies toekennen aan variabelen of doorgeven als argument aan andere functies. Bekijk bijvoorbeeld onderstaande drie functies.
def herhalen(waarde, functie, aantal): for i in range(aantal): waarde = functie(waarde) return waarde def verhogen(waarde): return waarde + 1 def verlagen(waarde): return waarde - 1
Hieronder staat een voorbeeld van hoe deze functies gebruikt kunnen worden. Ga na hoe Python reageert als je achtereenvolgens de volgende instructies uitvoert binnen een interactieve Python sessie waarin je eerst zorgt dat bovenstaande functies gedefinieerd werden. Verzeker jezelf ervan dat je goed begrijpt waarom je een bepaalde waarde krijgt en wat er juist gebeurt in de interactieve sessie vooraleer je verder gaat met de eigenlijke opgave.
>>> verhogen(5) >>> verlagen(101) >>> herhalen(5, verhogen, 3) >>> herhalen(5, verlagen, 3) >>> herhalen(5, verlagen, verhogen(3))
Opgave
- Schrijf drie functies blok, driehoek en gauss, die een implementatie vormen van de corresponderende signaalfuncties omschreven in de inleiding van deze opgave. Aan elke functie moeten twee argumenten doorgegeven worden: een afstand $r$ tussen een zendmast en een ontvangstpunt, en de sterkte $\alpha$ van de zendmast. Elke functie moet als resultaat de corresponderende ontvangststerkte teruggeven, als een reëel getal tussen 0 en 1.
- Schrijf een functie ontvangstkwaliteit die de gemiddelde ontvangstkwaliteit teruggeeft, gemeten over een reeks ontvangstpunten. De functie heeft twee verplichte parameters zendmasten en ontvangstpunten waaraan respectievelijk een lijst van coördinaten van zendmasten en een lijst van coördinaten van ontvangstpunten moeten doorgegeven worden. Elke coördinaat wordt daarbij voorgesteld als een tuple $(x, y)$. De functie heeft ook twee optionele parameters. Een parameter alfa die de sterkte $\alpha$ van de zendmasten (standaardwaarde 5.0) aangeeft, en een parameter signaalfunctie waaraan een signaalfunctie $f(r, \alpha)$ kan doorgegeven worden die het type van de zendmasten modelleert (standaard worden zendmasten gebruikt met een blokvormige sterkte).
Voorbeeld
>>> blok(1.0, 2.0) 1.0 >>> driehoek(1.0, 2.0) 0.5 >>> gauss(1.0, 2.0) 0.8824969025845955 >>> zendmasten = [(0.0, 0.0), (5.0, 5.0), (3.0, 4.0)] >>> ontvangstpunten = [(1.2, 4.3), (2.8, 3.3), (3.2, 0.7), (-1.0, -1.0), (10.0, 0.0)] >>> ontvangstkwaliteit(zendmasten, ontvangstpunten) 0.8 >>> ontvangstkwaliteit(zendmasten, ontvangstpunten, alfa=3.0) 0.6 >>> ontvangstkwaliteit(zendmasten, ontvangstpunten, signaalfunctie=driehoek) 0.5102911527511019 >>> ontvangstkwaliteit(zendmasten, ontvangstpunten, signaalfunctie=gauss) 0.8121116675748477
Hieronder zie je een kaartje dat de situatie toont voor het eerste geval in de bovenstaande doctest. Nadat je je oplossing hebt ingediend, kan je ook zo'n kaartjes bekijken om je te helpen bij het debuggen. Door te klikken op de ontvangstpunten of de zendmasten krijg je extra informatie te zien.
| Added by: | Peter Dawyndt |
| Date: | 2013-06-25 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS