SPOJ.com - Problem PROG0351

PROG0351 - Queens, knights and pawns

A number of queens, knights and pawns have been placed on a chessboard. Your task is to find out how many of the unoccupied squares on the board are not under attack from either a queen or a knight (or both). Such squares will be called safe squares. Pawns only serve to block maneuvers of queens. They can not perform attacks themselves.

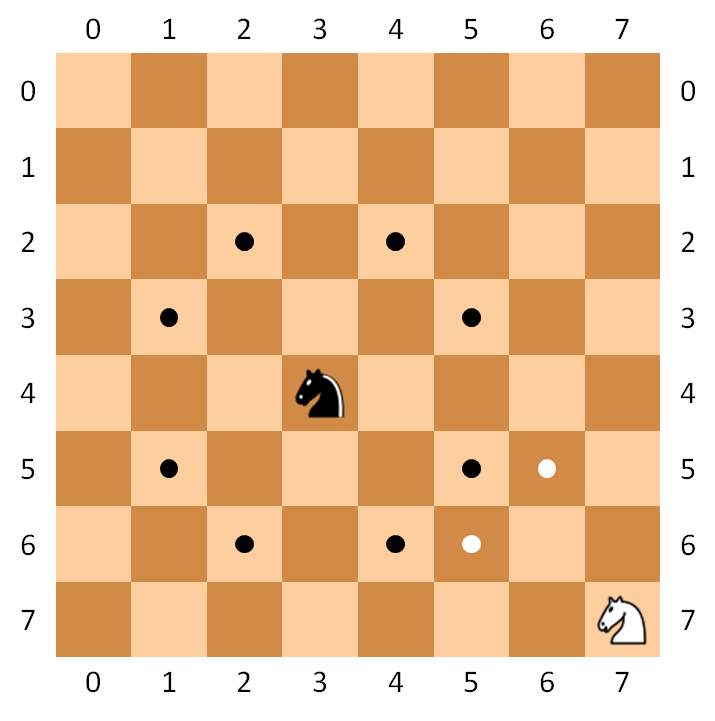
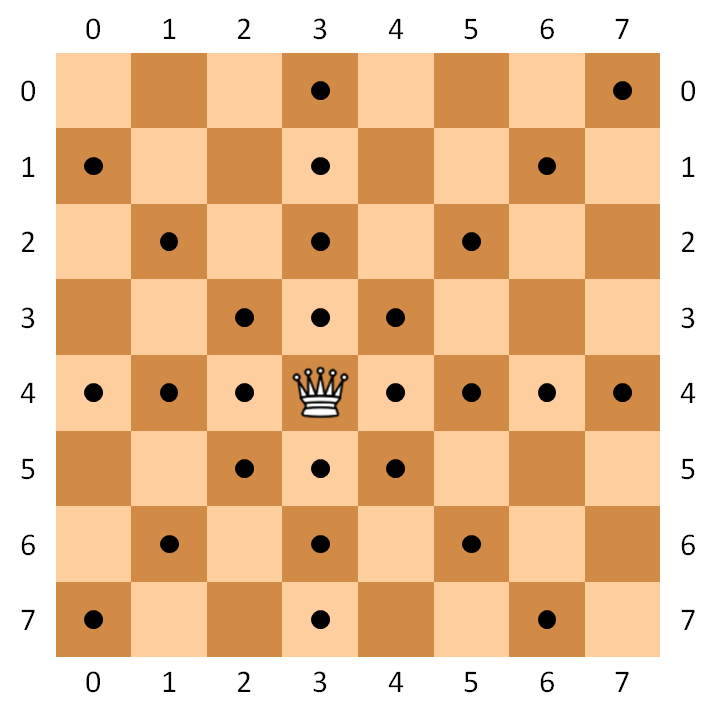
For those who are not familiar with the rules of chess, we recall that a knight can move to any unoccupied square that is on the opposite corner or a $2 \times 3$ rectangle from its current position. A queen can attack in any of the eight horizontal, vertical and diagonal directions from her current position. Note that the movement of a queen can be blocked by any other piece on the board, while a knight's movement can not be blocked by other pieces.

The black knight may attack any of eight squares that are marked by a black dot. The white knight is limited in attacking only the two squares marked by a white dot.

A queen can attack all squares in the horizontal, vertical and diagonal directions, marked by a black dot.

Assignment

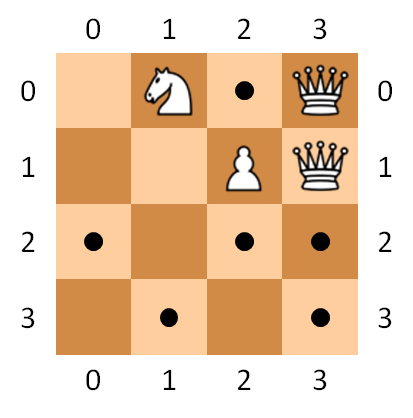
Write a function safeSquares that returns the number of safe squares on a given chessboard. The function takes three arguments. The first two arguments respectively indicate the number of rows $r \in \mathbb{N}$ and columns $c \in \mathbb{N}$ of the chessboard, where $r, c \geq 2$. The third argument is a list or a tuple that contains the positions of the pieces on the chessboard. The position of a piece is given by a list or a tuple containing three element. The first element is a string that described which kind of piece it is (Q represents a queen, K a knight and P a pawn). The second and third element give the row and column at which the piece is located. Rows and columns are numbered from zero, as with the chessboard in the above figures.

Example

>>> safeSquares(4, 4, (('K', 0, 1), ('Q', 0, 3), ('P', 1, 2), ('Q', 1, 3)))
6
>>> safeSquares(2, 3, (('Q', 0, 1), ('K', 0, 0)))
0
>>> safeSquares(8, 8, (('Q', 4, 3), ))
36
>>> safeSquares(8, 8, (('K', 4, 3), ('K', 7, 7)))
52

Op een schaakbord staan een aantal koninginnen, paarden en pionnen opgesteld. Je opdracht bestaat erin om te bepalen hoeveel onbezette vierkanten er zijn op het schaakbord die door geen enkele koningin en door geen enkel paard kunnen aangevallen worden. We noemen dit de veilige vierkanten van het schaakbord. Hierbij dienen de pionnen enkel om de bewegingsruimte van de koninginnen af te blokken. Ze kunnen zelf geen aanvallen uitvoeren.

Voor zij die de regels van het schaakspel niet kennen, geven we nog mee dat een paard elk onbezet vierkant van het schaakbord kan aanvallen dat gelegen is op het overstaande hoekpunt van een $2 \times 3$ rechthoek ten opzichte van zijn huidige positie. Een koningin kan een aanval uitvoeren op elk zichtbaar vierkant in elk van de acht horizontale, verticale of diagonale richtingen ten opzichte van zijn huidige positie. Merk hierbij op dat een aanvalsbeweging van een koningin afgeblokt wordt door elk ander stuk op het schaakbord, terwijl de aanval van een paard nooit door andere stukken kan geblokkeerd worden.

Het zwarte paard kan aanvallen uitvoeren naar elk van de acht vierkanten die zijn aangeduid met een zwarte cirkel. Het witte paard kan enkel aanvallen uitvoeren naar de twee vierkanten aangeduid met een witte cirkel.

Een koningin kan alle vierkanten aanvallen in horizontale, verticale en diagonale richting, hier aangeduid met een zwarte cirkel.

Opgave

Schrijf een functie veiligeVierkanten die teruggeeft hoeveel veilige vierkanten er zijn op een gegeven schaakbord. Aan deze functie moeten drie argumenten doorgegeven worden. De eerste twee argumenten geven respectievelijk het aantal rijen $r \in \mathbb{N}$ en kolommen $k \in \mathbb{N}$ van het schaakbord aan, waarbij steeds geldt dat $r, k \geq 2$. Het derde argument is een lijst of tuple dat de positie van de stukken op het schaakbord bevat. De positie van een stuk wordt omschreven door een lijst of tuple met drie elementen. Het eerste element is een string die aangeeft over welk soort stuk het gaat (Q voor koningin, K voor paard en P voor pion). Het tweede en derde element geven de rij en de kolom aan waarop het stuk zich bevindt. Rijen en kolommen worden hierbij steeds genummerd vanaf nul, zoals bij de schaakborden in bovenstaande afbeeldingen.

Voorbeeld

>>> veiligeVierkanten(4, 4, (('K', 0, 1), ('Q', 0, 3), ('P', 1, 2), ('Q', 1, 3)))
6
>>> veiligeVierkanten(2, 3, (('Q', 0, 1), ('K', 0, 0)))
0
>>> veiligeVierkanten(8, 8, (('Q', 4, 3), ))
36
>>> veiligeVierkanten(8, 8, (('K', 4, 3), ('K', 7, 7)))
52

Submit solution!

Added by:	Peter Dawyndt
Date:	2013-03-30
Time limit:	10s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	PY_NBC
Resource:	None

Informatics 1

PROG0351 - Queens, knights and pawns

Assignment

Example

Opgave

Voorbeeld