| Submit | All submissions | Best solutions | Back to list |
PROG0323 - Politeness |
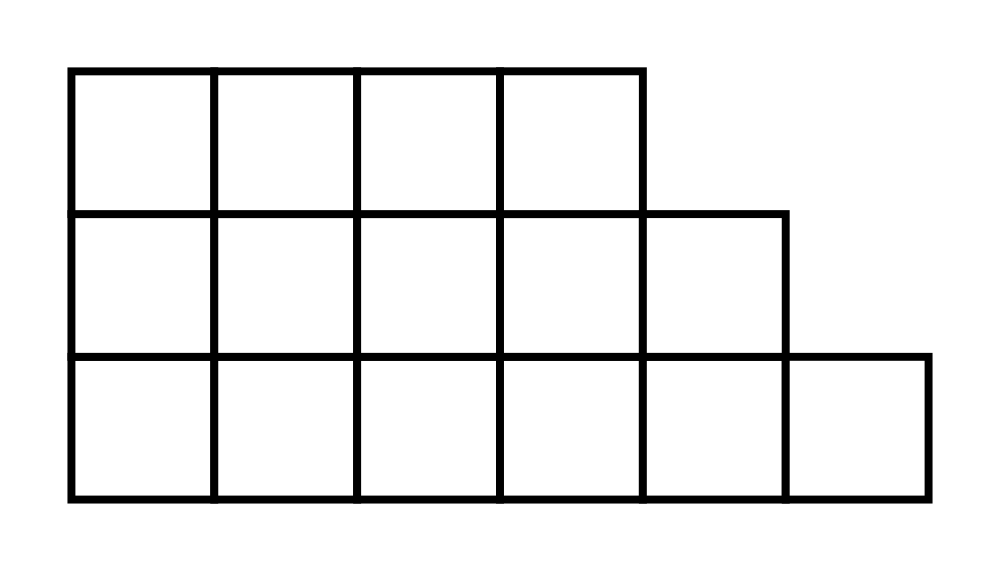
A strictly positive integer is polite if it can be written as the sum of two or more consecutive strictly positive integers. 7 is an example of a polite number as it can be written as 3+4. Polite numbers are sometimes also called staircase numbers because the Young diagrams, graphically representing the partitions of a polite number into consecutive integers, resemble staircases.
Some numbers can be written as a sum of consecutive numbers in multiple ways. 15, for example, can be written in three different ways:
1 + 2 + 3 + 4 + 5 4 + 5 + 6 7 + 8
The amount of ways in which a number can be written as a sum of two or more strictly positive integers, is called the politeness of a number. Numbers that are a power of two can't be written as a sum of two or more consecutive numbers. Those numbers have a politeness of 0, therefore they are impolite.
Input
A number $n \in \mathbb{N}_0$.
Output
A number that represents the politeness of the number $n$.
Example
Input:
15
Output:
3
Een strikt positief natuurlijk getal is beleefd als het kan geschreven worden als de som van twee of meer opeenvolgende strikt positieve natuurlijke getallen. Het getal 7 is bijvoorbeeld beleefd omdat het kan geschreven worden als 3 + 4. Beleefde getallen worden soms ook trapgetallen genoemd, omwille van de trapvorm van de Young diagrammen die een grafische voorstelling weergeven van de ontbinding van een beleefd getal in opeenvolgende natuurlijke getallen.
Sommige getallen kunnen op verschillende manieren geschreven worden als de som van twee of meer opeenvolgende getallen. Zo kan 15 bijvoorbeeld op de volgende manieren geschreven worden:
1 + 2 + 3 + 4 + 5 4 + 5 + 6 7 + 8
Het aantal manieren waarop een getal kan geschreven worden als de som van twee of meer opeenvolgende strikt positieve natuurlijke getallen wordt de beleefdheid van het getal genoemd. Elk getal dat een macht van twee is kan niet geschreven worden als de som van twee of meer opeenvolgende getallen. Dergelijke getallen hebben een beleefdheid van 0, en zijn dus onbeleefd.
Invoer
Een getal $n \in \mathbb{N}_0$.
Uitvoer
Een getal dat de beleefdheid van het getal $n$ aangeeft.
Voorbeeld
Invoer:
15
Uitvoer:
3
| Added by: | Peter Dawyndt |
| Date: | 2013-02-05 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS