| Submit | All submissions | Best solutions | Back to list |
PROG0302 - Dot plot |
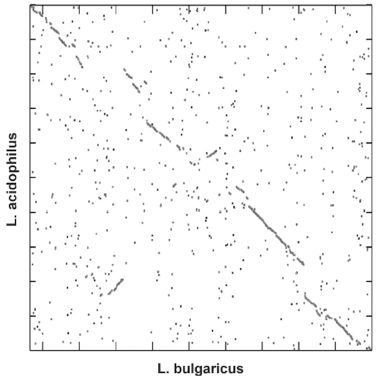
A dot plot is one of the oldest graphical representations to compare two biological sequences. Areas of two sequences that look alike a lot are visualized in a dot plot as diagonals.
Dot plots are built as two-dimensional matrices of which the rows correspond with the consecutive windows (this is the term that is used in this context for connected areas within a sequence) of the first sequence, and the columns with the consecutive windows from the second sequence. In the most simple shape, the windows are formed by the individual residues (letters) of a sequence, but in expansion, a window can also consist of $n$ consecutive residues. One cell of the matrix is made black (represented as the Boolean value True) if the corresponding window of the first sequence shows enough resemblance with the corresponding window from the second sequence. Otherwise, the cell from the matrix stays white (represented by the Boolean value False).
Assignment
Define a class Dotplot which can be used to make dot plots for two given biological sequences. Biological sequences are hereby represented as strings that only consist of letters from the alphabet (that represent the individual residues). Positions within these sequences are indexed from zero. Objects from the Dotplot must have the following methods:
- An initializing method to which two biological sequences as argument must be given as an argument. These sequences must be kept as attributes of the newly made object of the class Dotplot.
- A method windows with three parameters: i) a parameter start1 $\in \mathbb{N}$ that indicates a start position within the first sequence, ii) a parameter start2 $\in \mathbb{N}$ that indicates a start position within the second sequence, and iii) an optional parameter length $\in \mathbb{N}_0$ that indicates the length of a window (standard value 1). The method must print a tuple of two partial sequences that start at the respective start positions of the two sequence-attributes of the object, and have the given length as indicated by the parameter length. Deduce how the method must react if an invalid window size is given (a strictly positive number) from the example session, or if any windows from the given start positions can be cut from the given length.
- A method equal with four parameters: The same three parameters that are used by the method windows, and an optional parameter number $\in \mathbb{N}_0$ (standard value 1). The method must print a Boolean value as a result, that indicates if the number of equal similar residues (letters) of the windows that correspond with the first three parameters are larger than or equal to the value that was given to the parameter number. When comparing the residues, you may not make a distinction between uppercase and lowercase letters.
- A method plot that prints a two-dimensional matrix of a Boolean value. This matrix is represented as a list of lists, where the inner lists represents the rows of the matrix. The rows correspond with the consecutive windows from the first sequence attribute, and the columns correspond with the consecutive windows of the second sequence attribute. Windows have a set length (optional parameter length $\in \mathbb{N}_0$; standard value 1) and consecutive windows are a set number of positions away from each other (optional parameter step $\in \mathbb{N}_0$; the length of the windows is taken as the standard value). With these parameters, both overlapping and non-overlapping windows can be defined. A cell from the matrix gets the Boolean value True if the corresponding window from the first sequence shows enough similarity ( as defined by the method equal, combined with the optional parameter number $\in \mathbb{N}_0$; standard value 1) with the corresponding window from the second sequence. Otherwise, it gets the Boolean value False.
Example
Click the links in the example session below to see a graphical display of the dot plots.
>>> dotplot = Dotplot('ATCCTC', 'ATTCTCG') >>> dotplot.windows(start1=1, start2=4, length=3) ('TCC', 'TCG') >>> dotplot.windows(start1=1, start2=4, length=-3) Traceback (most recent call last): AssertionError: invalid window size >>> dotplot.windows(start1=1, start2=5, length=3) Traceback (most recent call last): AssertionError: invalid start position >>> dotplot.equal(start1=1, start2=4, length=3) True >>> dotplot.equal(start1=1, start2=4, length=3, number=2) True >>> dotplot.equal(start1=1, start2=4, length=3, number=3) False >>> dotplot.plot(length=1, step=1, number=1)[[True, False, False, False, False, False, False], [False, True, True, False, True, False, False], [False, False, False, True, False, True, False], [False, False, False, True, False, True, False], [False, True, True, False, True, False, False], [False, False, False, True, False, True, False]] >>> dotplot.plot(length=3, step=1, number=1)
Een dot plot is één van de oudste grafische voorstellingsvormen om twee biologische sequenties met elkaar te vergelijken. Gebieden van de twee sequenties die sterk op elkaar gelijken worden bij een dot plot immers gevisualiseerd als diagonalen.
Dot plots worden opgebouwd als tweedimensionale matrices waarvan de rijen overeenstemmen met de opeenvolgende vensters (dit is de term die in deze context gebruikt wordt voor aaneengesloten gebieden binnen een sequentie) van de eerste sequentie, en de kolommen met de opeenvolgende vensters van de tweede sequentie. In de meest eenvoudige vorm worden de vensters gevormd door de individuele residu's (letters) van een sequentie, maar bij uitbreiding kan een venster ook bestaat uit $n$ opeenvolgende residu's. Een cel van de matrix wordt zwart gemaakt (voorgesteld door de Booleaanse waarde True) indien het corresponderende venster van de eerste sequentie voldoende gelijkenis vertoont met het corresponderende venster van de tweede sequentie. Anders blijft de cel van de matrix wit (voorgesteld door de Booleaanse waarde False).
Opgave
Definieer een klasse Dotplot waarmee dot plots voor twee gegeven biologische sequenties kunnen aangemaakt worden. Biologische sequenties worden hierbij voorgesteld als strings die enkel bestaan uit letters van het alfabet (die de individuele residu's voorstellen). Posities binnen deze sequenties worden geïndexeerd vanaf nul. Objecten van de klasse Dotplot moeten volgende methoden hebben:
- Een initialisatiemethode waaraan twee biologische sequenties als argument moeten doorgegeven worden. Deze sequenties moeten als attributen van het nieuw aangemaakte object van de klasse Dotplot bijgehouden worden.
- Een methode vensters met drie parameters: i) een parameter start1 $\in \mathbb{N}$ die een startpositie binnen de eerste sequentie aangeeft, ii) een parameter start2 $\in \mathbb{N}$ die een startpositie binnen de tweede sequentie aangeeft, en iii) een optionele parameter lengte $\in \mathbb{N}_0$ die de lengte van een venster aangeeft (standaardwaarde 1). De methode moet een tuple van twee deelsequenties teruggeven die beginnen op de respectievelijke startposities van de twee sequentie-attributen van het object, en de opgegeven lengte hebben zoals aangegeven door de parameter lengte. Leid uit onderstaande voorbeeldsessie af hoe de methode moet reageren indien een ongeldige venstergrootte wordt opgegeven (een strikt positief geheel getal), of indien vanaf de opgegeven startposities geen vensters van de opgegeven lengte kunnen uitgeknipt worden.
- Een methode gelijk met vier parameters: dezelfde drie parameters die gebruikt worden door de methode vensters, en een optionele parameter aantal $\in \mathbb{N}_0$ (standaardwaarde 1). De methode moet een Booleaanse waarde als resultaat teruggeven, die aangeeft of het aantal gelijke overeenkomstige residu's (letters) van de vensters die corresponderen met de eerste drie parameters groter of gelijk is aan de waarde die werd doorgegeven aan de parameter aantal. Bij het vergelijken van residu's mag geen onderscheid gemaakt worden tussen hoofdletters en kleine letters.
- Een methode plot die een tweedimensionale matrix van Booleaanse waarden teruggeeft. Deze matrix wordt voorgesteld als een lijst van lijsten, waarbij de binnenste lijsten de rijen van de matrix voorstellen. De rijen corresponderen met de opeenvolgende vensters van het eerste sequentie-attribuut, en de kolommen met de opeenvolgende vensters van het tweede sequentie-attribuut. Vensters hebben een vaste lengte (optionele parameter lengte $\in \mathbb{N}_0$; standaardwaarde 1) en opeenvolgende vensters liggen een vast aantal posities van elkaar verwijderd (optionele parameter stap $\in \mathbb{N}_0$; als standaardwaarde wordt de lengte van de vensters genomen). Met deze parameters kunnen dus zowel overlappende als niet-overlappende vensters gedefinieerd worden. Een cel van de matrix krijgt de Booleaanse waarde True indien het corresponderende venster van de eerste sequentie voldoende gelijkenis (zoals gedefinieerd door de methode gelijk, in combinatie met de optionele parameter aantal $\in \mathbb{N}_0$; standaardwaarde 1) vertoont met het corresponderende venster van de tweede sequentie. Anders krijgt ze de Booleaanse waarde False.
Voorbeeld
Klik op de links in onderstaande voorbeeldsessie om een grafische voorstelling van de dot plots te bekijken.
>>> dotplot = Dotplot('ATCCTC', 'ATTCTCG') >>> dotplot.vensters(start1=1, start2=4, lengte=3) ('TCC', 'TCG') >>> dotplot.vensters(start1=1, start2=4, lengte=-3) Traceback (most recent call last): AssertionError: ongeldige venstergrootte >>> dotplot.vensters(start1=1, start2=5, lengte=3) Traceback (most recent call last): AssertionError: ongeldige startpositie >>> dotplot.gelijk(start1=1, start2=4, lengte=3) True >>> dotplot.gelijk(start1=1, start2=4, lengte=3, aantal=2) True >>> dotplot.gelijk(start1=1, start2=4, lengte=3, aantal=3) False >>> dotplot.plot(lengte=1, stap=1, aantal=1)
| Added by: | Peter Dawyndt |
| Date: | 2012-12-30 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |
RSS