| Submit | All submissions | Best solutions | Back to list |
PROG0281 - Language recognition |
The machine learning approach to teach a computer to recognize natural language consists of training models based on texts of reference for every existing language. The assumed language of a given text will be the one that best fits the model. In practice, reliable language processing through simple statistical models is already within reach.
The simple language model we will use here consists of a frequency table of all $n$-grams of a text file. A $n$-gram is just a series of $n$ successive characters on the same line. Before the $n$-grams of a line are determined, all uppercase letters must first be turned into lowercase letters, white space in front and at the end must be removed and white space between words must be replaced by one space. White space is defined as a series of consecutive spaces and tabs. Newlines are not taken into the $n$-gram. Note that spaces and punctuation marks are a part of the $n$-gram.
To determine how closely the $n$-gram based language model is to the $n$-gram based language model of the text of reference $r$ (note that in both cases the same length must e used for the $n$-grams), the following score is calculated: \[ s_r^n(t) = \sum_{m \in \mathcal{N}_t^n} f_t^n(m) \log\left(\frac{1 + f_r^n(m)}{c_r^n}\right) \] Here $\mathcal{N}_t^n$ is the collection of all $n$-grams of the text $t$, $f_t^n(m)$ (resp. $f_r^n(m)$) is the number of times the $n$-gram $m$ occurs in the text $t$ (resp. $r$), and $c_r^n$ is the total amount of $n$-grams in the text of reference $r$. $\log$ is the natural logarithm. The higher the score, the better the language model of the text fits the language model of the text of reference.
Assignment
- Write a function language_model that takes the location of a text file from which a simple language model can be trained. The function must return a dictionary that represents the frequency table of the language model as described in the introduction. The keys are formed by the $n$-grams of the text, and every $n$-gram is depicted by the dictionary according to the number of occurrences. As second optional argument that can be passed to the function is the value $n$ (by default the number of bigrams is calculated: $n=2$).
- Write a function similarity that determines how close the $n$-gram based language model of a text $t$ fits the $n$-gram based language model of a text of reference $r$. To this function two arguments must be passed, namely the dictionaries of the language model for the texts $t$ and $r$. The score must be returned as a floating point number by the function.
- Write a function languageprocessing with which the assumed language of a given text $t$ can be processed. As a fisrt argument, this function needs a dictionary that represents the language model of a given text $t$. The second argument that should be passed to the function is also a dictionary, with as a key a string with the description of a language and as corresponding value a dictionary with the language model that was determined based on a text of reference for that language. The function should return a tuple of which the two elements respectively are the description of the language (a string) and the score (a floating point number) that correspond with the language model from the dictionary — that was passed as second parameter — that best fits (highest score) text $t$. The language that corresponds with the highest score can be used as prediction of the language of the given text $t$.
Example
Click here to download a ZIP file that contains all files that are used on the examples below. The first example works with small files, so you can easily follow what is to be done.
>>> language_model('fruit.nl') {' b': 1, 'aa': 1, 'en': 1, 'ba': 1, 'n.': 1, 'ee': 1, 'na': 1, 'an': 2, 'n ': 1} >>> language_model('fruit.en', 3) {' ba': 1, 'ana': 2, 'a b': 1, 'na.': 1, 'nan': 1, 'ban': 1} >>> language_model('fruit.fr', 4) {'ne b': 1, 'une ': 1, 'e ba': 1, 'ane.': 1, 'nane': 1, 'bana': 1, 'anan': 1, ' ban': 1} >>> model_nl = language_model('fruit.nl') >>> model_en = language_model('fruit.en') >>> model_fr = language_model('fruit.fr') >>> similarity(model_nl, model_en) -16.11228418967414 >>> similarity(model_nl, model_fr) -18.7491848109244 >>> similarity(model_en, model_nl) -13.450867444376364 >>> models = {'en': model_en, 'fr': model_fr} >>> languageprocessing(model_nl, models) ('en', -16.11228418967414)
In the following example the language models are trained based on the text Universal Declaration of Human Rights. According to the Guiness Book of Records, this is the most translated document. Here we can conclude the the bigram "e•" (where • is a space) occurs resp. 352 and 330 times in the Dutch and English translation of the text. The trigram that occurs the most in the English version "the", i.e. 151 times. Despite the simplicity of the method, we find that the language of all text files can be determined properly.
>>> model_en = language_model('training.en', 3) >>> [(trigram, number) for trigram, number in model_en.items() if number == max(model_en.values())][0] ('the', 151) >>> model_en = language_model('training.en') >>> model_nl = language_model('training.nl') >>> model_fr = language_model('training.fr') >>> model_en['e '], model_fr['e '], model_nl['e '] (330, 509, 352) >>> text_en = language_model('test.en') >>> similarity(text_en, model_en) -230.33674380150703 >>> similarity(text_en, model_fr) -259.04854263587083 >>> similarity(text_en, model_nl) -261.7988606708526 >>> models = {'en': model_en, 'fr': model_fr, 'nl': model_nl} >>> languageprocessing(text_en, models) ('en', -230.33674380150703) >>> text_fr = language_model('test.fr') >>> languageprocessing(text_fr, models) ('fr', -129.8597104636806) >>> text_nl = language_model('test.nl') >>> languageprocessing(text_nl, models) ('nl', -185.44606662491037)
De machine learning-benadering om een computer de (natuurlijke) taal van een tekst te leren herkennen, bestaat er in modellen te trainen op basis van referentieteksten voor elke bestaande taal. De vermoedelijke taal van een gegeven tekst correspondeert dan met het model dat best aansluit bij die tekst. In de praktijk is het al mogelijk om betrouwbare taalherkenning te bekomen op basis van eenvoudige statistische modellen.
Het eenvoudige taalmodel dat we hier zullen gebruiken, bestaat uit de frequentietabel van alle $n$-grammen van een tekstbestand. Een $n$-gram is niets anders dan een reeks van $n$ opeenvolgende karakters die op eenzelfde regel voorkomen. Vóór de $n$-grammen van een regel bepaald worden, moet men eerst alle hoofdletters omzetten in kleine letters, witruimte vooraan en achteraan verwijderen, en witruimte tussen woorden telkens vervangen door één enkele spatie. Als witruimte beschouwen we een reeks opeenvolgende spaties en tabs. Eventuele newlines op het einde van een regel wordt nooit in een $n$-gram opgenomen. Merk op dat spaties en leestekens wel deel kunnen uitmaken van $n$-grammen.
Om te bepalen hoe dicht het $n$-gram gebaseerde taalmodel van een tekst $t$ aansluit bij het $n$-gram gebaseerde taalmodel van een referentietekst $r$ (merk dus op dat in beide gevallen dezelfde lengte voor de $n$-grammen moet gebruikt worden), wordt de volgende score berekend: \[ s_r^n(t) = \sum_{m \in \mathcal{N}_t^n} f_t^n(m) \log\left(\frac{1 + f_r^n(m)}{c_r^n}\right) \] Hierbij stelt $\mathcal{N}_t^n$ de verzameling van alle $n$-grammen van de tekst $t$ voor, stelt $f_t^n(m)$ (resp. $f_r^n(m)$) het aantal voorkomens van het $n$-gram $m$ in de tekst $t$ (resp. $r$) voor, en stelt $c_r^n$ het totaal aantal $n$-grammen in de referentietekst $r$ voor. $\log$ staat voor de natuurlijke logaritme. Hoe hoger de score, hoe beter het taalmodel van de tekst aansluit bij het taalmodel van de referentietekst.
Opgave
- Schrijf een functie taalmodel waaraan de locatie van een tekstbestand moet doorgegeven worden, waarmee een eenvoudige taalmodel kan getraind worden. De functie moet als resultaat een dictionary teruggeven, die de frequentietabel van het taalmodel voorstelt zoals beschreven in de inleiding. Daarbij worden de sleutels dus gevormd door de $n$-grammen van de tekst, en wordt elk $n$-gram door de dictionary afgebeeld op zijn aantal voorkomens. Als tweede optionele argument kan aan de functie een waarde voor $n$ doorgegeven worden (standaard wordt het aantal bigrammen geteld: $n=2$).
- Schrijf een functie overeenkomst die bepaalt hoe dicht het $n$-gram gebaseerde taalmodel van een tekst $t$ aansluit bij het $n$-gram gebaseerde taalmodel van een referentietekst $r$. Aan deze functie moeten twee argumenten doorgegeven worden, namelijk de dictionaries van het taalmodel voor de teksten $t$ en $r$. De score moet door de functie als een floating point getal teruggegeven worden.
- Schrijf een functie taalherkenning waarmee de vermoedelijke taal van een gegeven tekst $t$ kan herkend worden. Als eerste argument moet aan deze functie een dictionary doorgegeven worden, die het taalmodel van een gegeven tekst $t$ voorstelt. Het tweede argument dat aan de functie moet doorgegeven worden is ook een dictionary, met telkens als sleutel een string met de omschrijving van een taal en als corresponderende waarde een dictionary met het taalmodel dat bepaald werd op basis van een referentietekst voor die taal. De functie moet als waarde een tuple teruggeven, waarvan de twee elementen respectievelijk de omschrijving van de taal (een string) en de score (een floating point getal) zijn die corresponderen met het taalmodel uit de dictionary — die als tweede parameter werd doorgegeven — dat het dichtst aansluit (hoogste score) bij de tekst $t$. De taal die correspondeert met de hoogste score kan gebruikt worden als voorspelling van de taal van de gegeven tekst $t$.
Voorbeeld
Klik hier om een ZIP bestand te downloaden dat alle bestanden bevat die in onderstaande voorbeelden gebruikt worden. Het eerste voorbeeld werkt met kleine bestanden, zodat je makkelijk kunt volgen wat er moet gebeuren.
>>> taalmodel('fruit.nl') {' b': 1, 'aa': 1, 'en': 1, 'ba': 1, 'n.': 1, 'ee': 1, 'na': 1, 'an': 2, 'n ': 1} >>> taalmodel('fruit.en', 3) {' ba': 1, 'ana': 2, 'a b': 1, 'na.': 1, 'nan': 1, 'ban': 1} >>> taalmodel('fruit.fr', 4) {'ne b': 1, 'une ': 1, 'e ba': 1, 'ane.': 1, 'nane': 1, 'bana': 1, 'anan': 1, ' ban': 1} >>> model_nl = taalmodel('fruit.nl') >>> model_en = taalmodel('fruit.en') >>> model_fr = taalmodel('fruit.fr') >>> overeenkomst(model_nl, model_en) -16.11228418967414 >>> overeenkomst(model_nl, model_fr) -18.7491848109244 >>> overeenkomst(model_en, model_nl) -13.450867444376364 >>> modellen = {'en':model_en, 'fr':model_fr} >>> taalherkenning(model_nl, modellen) ('en', -16.11228418967414)
In onderstaand voorbeeld worden taalmodellen getraind op basis van de tekst van de Universele verklaring van de rechten van de mens. Volgens het Guinness Recordboek is dit het document dat naar het meest aantal talen werd vertaald. Hieruit leiden we af dat het bigram "e•" (hierbij stelt • een spatie voor) resp. 352 en 330 keer voorkomt in de Nederlandse en Engelse vertaling van de tekst. Het trigram dat het vaakst voorkomt in de Engelse vertaling is "the", zijnde 151 keer. Ondanks de eenvoud van de methode, stellen we toch vast dat de taal van alle testbestanden correct herkend wordt.
>>> model_en = taalmodel('training.en', 3) >>> [(trigram, aantal) for trigram, aantal in model_en.items() if aantal == max(model_en.values())][0] ('the', 151) >>> model_en = taalmodel('training.en') >>> model_nl = taalmodel('training.nl') >>> model_fr = taalmodel('training.fr') >>> model_en['e '], model_fr['e '], model_nl['e '] (330, 509, 352) >>> tekst_en = taalmodel('test.en') >>> overeenkomst(tekst_en, model_en) -230.33674380150703 >>> overeenkomst(tekst_en, model_fr) -259.04854263587083 >>> overeenkomst(tekst_en, model_nl) -261.7988606708526 >>> modellen = {'en':model_en, 'fr':model_fr, 'nl':model_nl} >>> taalherkenning(tekst_en, modellen) ('en', -230.33674380150703) >>> tekst_fr = taalmodel('test.fr') >>> taalherkenning(tekst_fr, modellen) ('fr', -129.8597104636806) >>> tekst_nl = taalmodel('test.nl') >>> taalherkenning(tekst_nl, modellen) ('nl', -185.44606662491037)
| Added by: | Peter Dawyndt |
| Date: | 2012-09-05 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

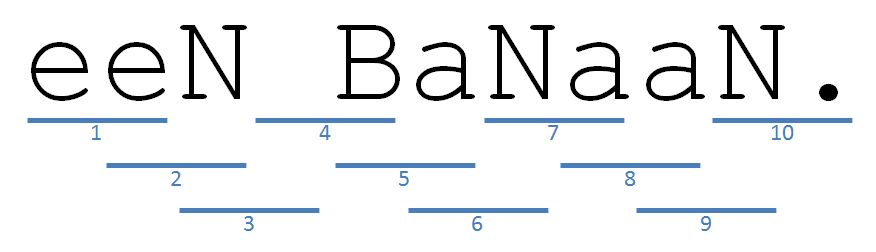
 RSS
RSS