SPOJ.com - Problem PROG0214

PROG0214 - Drawing polymers

In the previous assignment, we have represented a polymer as a list containing the positions of the successive monomers of the polymer. Each position is represented as a tuple $(x,y)$, where $x,y \in \mathbb{Z}$. The first monomer is always placed at the origin $(0,0)$ of the Cartesian plane, and the next position is always one unit step up, down, left or right of the previous position. Two monomers of the same polymer can never occupy the same position.

Assignment

Write a function showPolymer which prints the structure of a polymer for a given list of positions of the monomers of a polymer (which is to be passed to the function as argument). To do this, just follow these steps:

Define a two-dimensional matrix $P$ (such as a list of lists) to build the structure of the polymer in. Initially all the elements of this matrix contain a string consisting of a single space.
The even rows and columns of the matrix are used to indicate where the monomers of the polymer are located. Monomers are indicated by the letter o, with the exception of the first monomer that is designated by the letter x and the last monomer which is indicated with an asterisk (*). For each monomer at position $(x,y)$ the space in the matrix at position $P_{i,j}$ is replaced by the character that represents the monomer, wherein
\[\begin{cases}
\, i = 2\,(y_{\max} - y) \\
\, j = 2\,(x - x_{\min})
\end{cases}
\]if we assume that the rows and columns of the matrix are indexed from 0. Here $x_{\min}$ is the minimum $x$-co-ordinate of all monomers in the polymer, and $y_{\max}$ is the maximum $y$-co-ordinate of all the monomers in the polymer.
On the odd-numbered rows and columns of the matrix, we connect the successive monomers of the polymer with each other. Two consecutive monomers that are left and right of each other, are connected by a hyphen (-) bridge between the two positions of the monomers in the matrix. Two consecutive monomers above and below each other are connected by a vertical bar (|). After the preceding steps, the matrix that corresponds to the list representation of the polymer
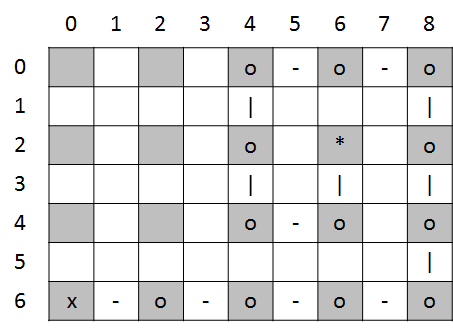
```
(0, 0), (1, 0), (2, 0), (3, 0), (4, 0), (4, 1), (4, 2), 
(4, 3), (3, 3), (2, 3), (2, 2), (2, 1), (3, 1), (3, 2)
```
looks like

matrix representation of a random walk

The empty cells in the matrix representation still contain a string that consists of a single space.
The output is generated by printing the rows of the matrix one by one (from top to bottom), in which the various characters in the columns of the same row are written one after the other. The preceding example then delivers the following output.
```
    o-o-o
    |   |
    o * o
    | | |
    o-o o
        |
x-o-o-o-o
```

Example

>>> polymer1 = [(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (1, 2), (0, 2), 
...              (0, 1), (1, 1)]
>>> showPolymer(polymer1)
o-o-o
|   |
o-* o
    |
x-o-o
>>> polymer2 = [(0, 0), (1, 0), (2, 0), (2, -1), (3, -1), (4, -1), (4, 0), 
...              (4, 1), (3, 1), (3, 0)]
>>> showPolymer(polymer2)
      o-o
      | |
x-o-o * o
    |   |
    o-o-o
>>> polymer3 = [(0, 0), (0, -1), (1, -1), (1, -2), (1, -3), (1, -4), (0, -4), 
...              (0, -3), (-1, -3), (-2, -3), (-2, -2), (-2, -1), (-1, -1), 
...              (-1, -2), (0, -2)]
>>> showPolymer(polymer3)
    x  
    |  
o-o o-o
| |   |
o o-* o
|     |
o-o-o o
    | |
    o-o

In de vorige opgave hebben we een polymeer voorgesteld als een lijst die de posities van de opeenvolgende monomeren van het polymeer bevat. Elke positie wordt hierbij voorgesteld als een tuple $(x,y)$, waarbij $x,y \in \mathbb{Z}$. Het eerste monomeer ligt telkens in de oorsprong $(0,0)$ van het cartesisch vlak, en de volgende positie ligt telkens één eenheidsstap boven, onder, links of rechts van de vorige positie. Twee monomeren van eenzelfde polymeer kunnen nooit dezelfde positie bezetten.

Opgave

Schrijf een functie toonPolymeer die voor een gegeven lijst van posities van de monomeren van een polymeer (die als argument aan de functie moet doorgegeven worden) de structuur van het polymeer uitschrijft. Hiervoor ga je als volgt te werk:

Definieer een 2-dimensionale matrix $P$ (bijvoorbeeld als een lijst van lijsten) om de structuur van het polymeer in op te bouwen. Initieel bevatten alle elementen van deze matrix een string die bestaat uit één enkele spatie.
De even rijen en kolommen van de matrix worden gebruikt om aan te geven waar de monomeren van het polymeer zich bevinden. Monomeren worden aangeduid met de kleine letter o, met uitzondering van het eerste monomeer dat wordt aangeduid met de letter x en het laatste monomeer dat wordt aangeduid met een sterretje (*). Voor elk monomeer op positie $(x,y)$ wordt de spatie in de matrix op positie $P_{i,j}$ vervangen door het karakter dat het monomeer voorstelt, waarbij\[\begin{cases}
\, i = 2\,(y_{\max} - y) \\
\, j = 2\,(x - x_{\min})
\end{cases}
\]als we ervan uitgaan dat de rijen en kolommen van de matrix geïndexeerd worden vanaf 0. Hierbij stelt $x_{\min}$ de minimale $x$-coördinaat van alle monomeren in het polymeer voor, en is $y_{\max}$ de maximale $y$-coördinaat van alle monomeren in het polymeer.
Op de oneven rijen en kolommen van de matrix verbinden we de opeenvolgende monomeren van het polymeer met elkaar. Twee opeenvolgende monomeren die links en rechts van elkaar liggen worden verbonden door een koppelteken (-) tussen de twee posities van de monomeren in de matrix te plaatsen. Twee opeenvolgende monomeren die boven en onder elkaar liggen worden verbonden door een verticale streep (|). Na voorgaande stappen, ziet de matrix die overeenkomt met de lijstvoorstelling van het polymeer
```
(0, 0), (1, 0), (2, 0), (3, 0), (4, 0), (4, 1), (4, 2), 
(4, 3), (3, 3), (2, 3), (2, 2), (2, 1), (3, 1), (3, 2)
```
er dan bijvoorbeeld als volgt uit

matrixvoorstelling van random walk

De lege cellen in deze matrixvoorstelling bevatten nog steeds een string die bestaat uit één enkele spatie.
De uitvoer wordt gegenereerd door de rijen van de matrix één voor één uit te schrijven (van boven naar onder), waarbij de verschillende karakters in de kolommen van eenzelfde rij achter elkaar uitgeschreven worden. Het voorgaande voorbeeld levert dan volgende uitvoer op.
```
    o-o-o
    |   |
    o * o
    | | |
    o-o o
        |
x-o-o-o-o
```

Voorbeeld

>>> polymeer1 = [(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (1, 2), (0, 2), 
...              (0, 1), (1, 1)]
>>> toonPolymeer(polymeer1)
o-o-o
|   |
o-* o
    |
x-o-o
>>> polymeer2 = [(0, 0), (1, 0), (2, 0), (2, -1), (3, -1), (4, -1), (4, 0), 
...              (4, 1), (3, 1), (3, 0)]
>>> toonPolymeer(polymeer2)
      o-o
      | |
x-o-o * o
    |   |
    o-o-o
>>> polymeer3 = [(0, 0), (0, -1), (1, -1), (1, -2), (1, -3), (1, -4), (0, -4), 
...              (0, -3), (-1, -3), (-2, -3), (-2, -2), (-2, -1), (-1, -1), 
...              (-1, -2), (0, -2)]
>>> toonPolymeer(polymeer3)
    x  
    |  
o-o o-o
| |   |
o o-* o
|     |
o-o-o o
    | |
    o-o

Submit solution!

Added by:	Peter Dawyndt
Date:	2012-02-01
Time limit:	10s-15s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	PY_NBC
Resource:	None

Informatics 1

PROG0214 - Drawing polymers

Assignment

Example

Opgave

Voorbeeld