SPOJ.com - Problem PROG0092

PROG0092 - Growth chart

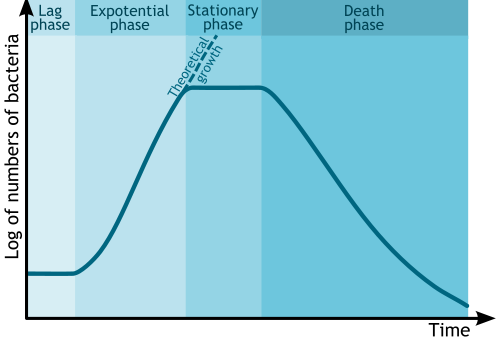
To draw up a bacterial growth chart $y = f(t)$, the amount of bacterial cells $y_i$ is determined spectrophotometrically on a regular basis $t_i$ ($i = 1, \ldots, n$).

To determine change in the growth chart, the derivative of the measured curve can be stipulated. Based on the derivative function, we learn where increasing and decreasing trends can be noticed and where the curve peaks. To determine an estimate of the derivative $y_i' = f'(t_i)$ at a time $t_i$ ($1 < i < n$), one can use a formula for numeral derivation: $$ y'_i = f'(t_i) = \frac12 \left(\frac{y_{i+1}-y_i}{t_{i+1}-t_i}+\frac{y_i-y_{i-1}}{t_i-t_{i-1}}\right) $$

Input

The input consists of 100 lines with two decimals $t_i$ and $y_i$ ($1 \leq i \leq 100$) on each line. Both values are always separated by a single space. This data represents the measurements of the growth chart $y = f(t)$ for the consecutive points in time. $t_i$. $t_i < t_j$ if $i < j$ is always true.

Output

Print a line for every measurement $t_i$, stating the value $t_i$ and an estimate of the derivative $y'_i = f'(t_i)$, separated by a single space. In the outer points of the measuring data, there isn't enough information about the curve $y = f(x)$ to estimate the derivative. In this case, write a hyphen (- ), instead of the value for the derivative.

Example

Input:

0.5 1
2 2
4 3
5.1 3.14
... ## and so on

Output:

0.5 -
2.0 0.583333333333
4.0 0.313636363636
... ## and so on

Om een bacteriële groeicurve $y = f(t)$ te bepalen, wordt op regelmatige tijdstippen $t_i$ ($i = 1, \ldots, n$) het aantal bacteriële cellen $y_i$ spectrofotometrisch bepaald.

Om na te gaan waar er zich veranderingen voordoen in de groeicurve, kan de afgeleide van de gemeten curve bepaald worden. Aan de hand van de afgeleide functie leren we waar er stijgende en dalende trends merkbaar zijn, en waar er zich pieken in de curve voordoen. Om een benadering van de afgeleide $y_i' = f'(t_i)$ op tijdstip $t_i$ ($1 < i < n$) te bepalen, kan gebruik gemaakt worden van de formule voor numerieke afgeleiding: $$ y'_i = f'(t_i) = \frac12 \left(\frac{y_{i+1}-y_i}{t_{i+1}-t_i}+\frac{y_i-y_{i-1}}{t_i-t_{i-1}}\right) $$

Invoer

De invoer bestaat uit 100 regels met op elke regel twee decimale getallen $t_i$ en $y_i$ ($1 \leq i \leq 100$). De twee waarden worden telkens van elkaar gescheiden door één enkele spatie. Deze gegevens stellen metingen van de groeicure $y = f(t)$ voor op opeenvolgende tijdstippen $t_i$. Er geldt dus steeds dat $t_i < t_j$ als $i < j$.

Uitvoer

Schrijf voor elk meetpunt $t_i$ een regel naar de uitvoer, met daarop de waarde $t_i$ en een benadering van de afgeleide $y'_i = f'(t_i)$, van elkaar gescheiden door één enkele spatie. In de eindpunten van de meetgegevens is er niet voldoende informatie over de curve $y = f(x)$ beschikbaar om de afgeleide te kunnen benaderen. In dat geval moet een koppelteken (- ) uitgeschreven worden in plaats van een waarde voor de afgeleide.

Voorbeeld

Invoer:

0.5 1
2 2
4 3
5.1 3.14
... ## enzoverder

Uitvoer:

0.5 -
2.0 0.583333333333
4.0 0.313636363636
... ## enzoverder

Submit solution!

Added by:	Peter Dawyndt
Date:	2011-08-03
Time limit:	10s
Source limit:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)
Languages:	PY_NBC
Resource:	None

Informatics 1