| Submit | All submissions | Best solutions | Back to list |
PROG0068 - Plancks law |
In astronomy, Planck's law describes the electromagnetic radiation emitted by a black body in the thermal equilibrium at a definite temperature: $$\rho(T,\lambda) = \frac{8\pi hc}{\lambda^5}\frac{1}{e^{\frac{hc}{\lambda k T}}- 1}$$ Here, $T$ is the temperature (in Kelvin), $\lambda$ is the wavelength (in metre), $h$ is the constant of Planck ($6,62608 \times 10^{-34}$ Js), $c$ the light speed ($2,99792458 \times 10^8$ ms$^{-1}$), and $k$ is the constant of Boltzmann ($1,38066 \times 10^{-23}$ JK$^{-1}$).
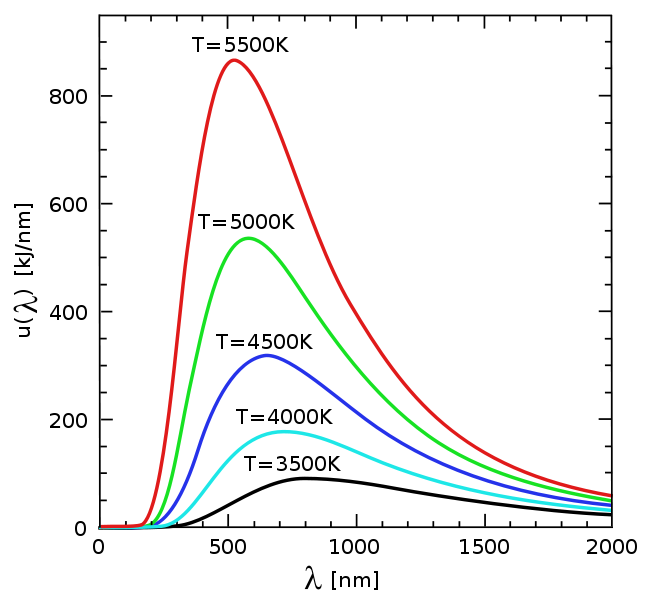
Hint: Compare the output of your program with the picture below (source: Wikipedia):
Input
The input consists of $t$ test cases ($t \leq 50$). The first line of the input contains an integer $t$. Then, $t$ lines follow that describe the different test cases. For every test case, the input contains two lines. The first line contains a given temperature $T$ expressed in Kelvin. The second line contains a given wavelength $\lambda$ expressed in micrometre (1 micrometre = $10^{-6}$ metre).
Output
For every test case, the energy density $\rho$ in SI units (this is Joule per m$^4$) that corresponds with the given temperature $T$ and wavelength $\lambda$.
Example
Input:
5 5500 0.5 4500 0.5 3500 0.5 5000 1.0 4000 1.0
Output:
858255.480667 267354.545955 42955.5563284 297696.258875 140690.424377
In de sterrenkunde wordt de energiedichtheid van een zwarte straler per tijdseenheid en per eenheid van golflengte bepaald door de stralingsenergieformule van Planck: $$\rho(T,\lambda) = \frac{8\pi hc}{\lambda^5}\frac{1}{e^{\frac{hc}{\lambda k T}}- 1}$$ Hierbij is $T$ de temperatuur (uitgedrukt in Kelvin), $\lambda$ de golflengte (uitgedrukt in meter), $h$ de constante van Planck ($6,62608 \times 10^{-34}$ Js), $c$ de lichtsnelheid ($2,99792458 \times 10^8$ ms$^{-1}$), en $k$ de constante van Boltzmann ($1,38066 \times 10^{-23}$ JK$^{-1}$).
Hint: Controleer de uitvoer van je programma aan de hand van onderstaande figuur (bron: Wikipedia):
Invoer
De invoer bestaan uit $t$ testgevallen ($t \leq 50$). De eerste regel van de invoer bevat een natuurlijk getal $t$. Daarna volgen $t$ regels die de verschillende testgevallen omschrijven. Voor elk testgeval bevat de invoer twee regels. De eerste regel bevat een gegeven temperatuur $T$ uitgedrukt in Kelvin. De tweede regel bevat een gegeven golflengte $\lambda$ uitgedrukt in micrometer (1 micrometer = $10^{-6}$ meter).
Uitvoer
Voor elk testgeval de energiedichtheid $\rho$ in SI-eenheden (dit is Joule per m$^4$) die correspondeert met de gegeven temperatuur $T$ en golflengte $\lambda$.
Voorbeeld
Invoer:
5 5500 0.5 4500 0.5 3500 0.5 5000 1.0 4000 1.0
Uitvoer:
858255.480667 267354.545955 42955.5563284 297696.258875 140690.424377
| Added by: | Peter Dawyndt |
| Date: | 2011-07-27 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | PY_NBC |
| Resource: | None |

 RSS
RSS