| Nộp bài | Các bài nộp | Làm tốt nhất | Về danh sách bài |
PTIT134G - Công thức Faulhaber |
Trong toán học, công thức Faulhaber về tổng chuỗi số như sau:
Cho chuỗi số : S(n,p) = 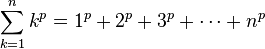
Tổng chuỗi số trên có thể biểu diễn thành một đa thức bậc p + 1 của n.
Đó là:
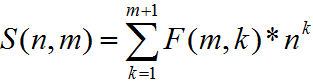
Ví dụ:
S(n, 1) = (1 + ... + n) = (1/2) * n2 + (1/2) * n
S(n, 2) = (1 + ... + n2) = (1/3) * n3 + (1/2) * n2 + (1/6) * n
S(n, 3) = (1 +...+ n3) = (1/4) * n4 + (1/2) * n3) + (1/4) * n2
S(n, 4) = (1 +...+ n4) = (1/5) * n5 + (1/2) * n4) + (1/3) * n3 - (1/30) * n
Các hệ số F(m,k) xây dựng lên thành tam giác Faulhaber:
1
1/2 1/2
1/6 1/2 1/3
0 1/4 1/2 1/4
-1/30 0 1/3 1/2 1/5
0 -1/12 0 5/12 1/2 1/6
1/42 0 -1/6 0 1/2 1/2 1/7
trong đó m bắt đầu từ 0, và k chạy từ 1 tới m + 1 (hàng m có m + 1 phần tử).
Quy luật xây dựng tam giác Faulhaber như sau:
1) Phần tử hàng i, cột j (j>1): F(i,j) = (i / j) * F(i-1, j-1).
2) Phần tử F(i,1) được lựa chọn sao cho tổng tất cả các phần tử hàng F(i,j) = 1.
Nhiệm vụ của bạn là xác định phần tử của tam giác Faulhaber dưới dạng tối giản.
Input
Dòng đầu tiên là số bộ test. (<= 1000)
Các dòng tiếp theo, mỗi dòng gồm 3 số.
Số đầu tiên là số thứ tự của bộ test. 2 số tiếp theo là m và k (1 <= m <= 400).
Output
Với mỗi test, in ra trên 1 dòng 2 số: số thứ tự của bộ test và phần tử F(m, k) dưới dạng tối giản.
(Nếu là số nguyên thì để nguyên, nếu là phân số thì rút gọn thành phân số tối giản).
Example
Input:
4 1 4 1 2 4 3 3 86 79 4 400 401Output:
1 -1/30 2 1/3 3 -22388337 4 1/401
| Được gửi lên bởi: | adm |
| Ngày: | 2013-02-28 |
| Thời gian chạy: | 3s |
| Giới hạn mã nguồn: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Ngôn ngữ cho phép: | ASM32-GCC ASM32 MAWK BC C CSHARP C++ 4.3.2 CPP CPP14 COFFEE LISP sbcl DART FORTH GO JAVA JS-RHINO JS-MONKEY KTLN OCT PAS-GPC PAS-FPC PERL PERL6 PROLOG PYTHON PYTHON3 PY_NBC R RACKET SQLITE SWIFT UNLAMBDA |

