| Nộp bài | Các bài nộp | Làm tốt nhất | Về danh sách bài |
P197PROI - Problem I – BST |
Cây nhị phân tìm kiếm là một cấu trúc dữ liệu dạng cây, trong đó mỗi nút được gán một giá trị và có nhiều nhất hai nút con. Giá trị của mỗi nút luôn lớn hơn giá trị của nút con trái và nhỏ hơn giá trị của nút con phải. Nút không có nút con được gọi là nút lá. Độ cao của cây được định nghĩa là số nút trên đường đi đơn từ nút gốc tới nút lá xa nhất.
Hãy đếm số lượng các cây nhị phân tìm kiếm khác nhau thoả mãn các điều kiện sau:
- Cây gồm N nút.
- Giá trị các nút là các số nguyên dương không vượt quá M (N ≤ M).
- Giá trị các nút là phân biệt.
- Độ cao của cây không nhỏ hơn H (H ≤ N).
Input
Dòng đầu tiên gồm 1 số nguyên T là số lượng bộ test.
T dòng tiếp theo, mỗi dòng gồm 3 số nguyên N, M, H (1 ≤ H ≤ N ≤ 80, N ≤ M ≤ 160).
Output
Với mỗi bộ test, in ra kết quả là số cây nhị phân tìm kiếm thoả mãn điều kiện, modulo 1012 + 9.
Example
Input: 2 2 3 2 3 3 2 Output: 6 5
Giải thích
Các trường hợp thoả mãn của test thứ 2:
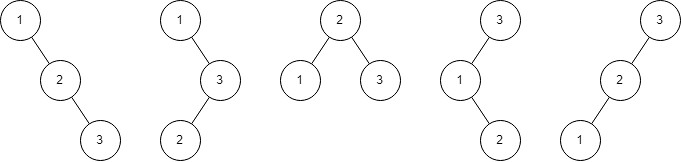
| Được gửi lên bởi: | adm |
| Ngày: | 2019-03-30 |
| Thời gian chạy: | 1s |
| Giới hạn mã nguồn: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Ngôn ngữ cho phép: | ASM32-GCC ASM32 ASM64 MAWK BC C CSHARP C++ 4.3.2 CPP CPP14 COFFEE LISP sbcl DART FORTH GO JAVA JS-RHINO JS-MONKEY KTLN OCT PAS-GPC PAS-FPC PERL PERL6 PROLOG PYTHON PYTHON3 PY_NBC R RACKET SQLITE SWIFT UNLAMBDA |

