| Submit | All submissions | Best solutions | Back to list |
PROG0236 - Intersection of rectangles |
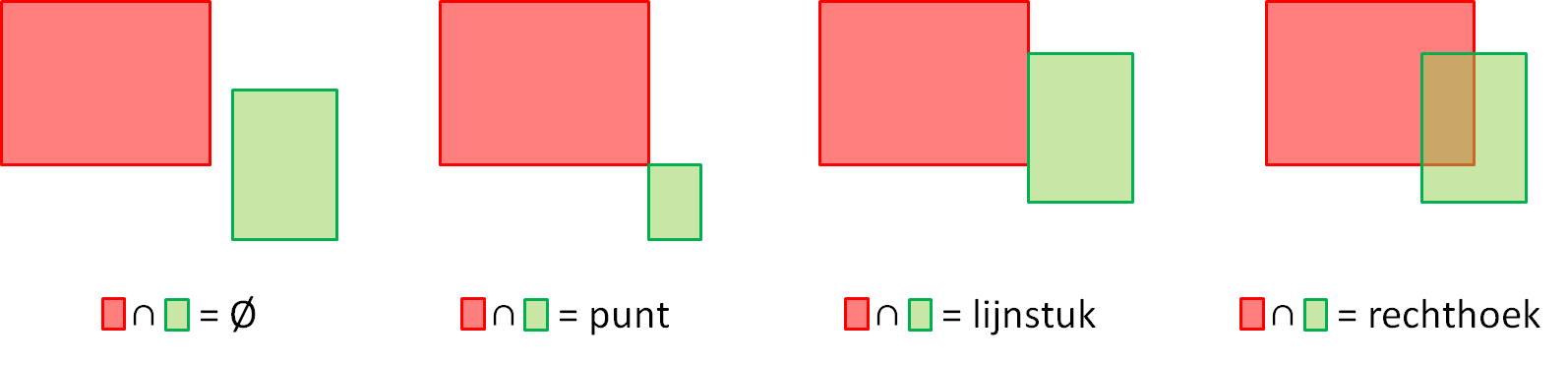
If we want to determine the intersection of two given rectangles in the Euclidean surface, there are four possibilities. The intersection is either empty, a point (common vertices), a line segment or a rectangle.
Assignment
Define a class Point with which points in the Euclidean surface with whole co-ordinates can be represented. This class must support the following methods:
- An initializing method __init__ that allows to make a point in the Euclidean surface based on a $x$ and $y$ co-ordinates. Both co-ordinates can be given to the method as the optional parameters x and y ($x, y \in \mathbb{Z}$), and have a value zero if they weren't given. The initializing method must appoint the given values or their standard values to the attributes x and y of the newly made object.
- Methods __str__ and __repr__ that both print a string representation of a point given in the format "Point(x, y)", where x and y respectively represent the $x$ and $y$ co-ordinate of the point in the Euclidean surface.
- Methods __lt__, __le__, __eq__, __ne__, __gt__ and __ge__ that allow to compare two points from the Euclidean surface using the Python operators <, <=, ==, !=, > and >=. The comparison of two points happens by first comparing their $x$ co-ordinates, and then the $y$ co-ordinates if the $x$ co-ordinates are equal.
- A method distance that can be used to calculate the Euclidean distance between two points in the Euclidean surface. The Euclidean distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by \[ \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \]
Define a class Linesegment that can be used to represent the line segments in the Euclidean surface that have a length larger than zero. This class must support the following methods:
- An initializing method __init__ that allows to make a line segment in the Euclidean surface based on two given points. Two object of the class Point must be given to this method, that represent both ends of the line segment. The smallest of these points must be appointed to the attribute point1 of the newly made object by the initializing method, and the largest point to the attribute point2. Watch the example below to verify which action the initializing method should take if the given line segment has length zero.
- Methods __str__ and __repr__ that both print a string representation of the format "Linesegment(Point(x1, y1), Point(x2, y2))", where x1 and y1 respectively represent the $x$ and $y$ co-ordinate of the smallest endpoint of the line segment and x2 and y2 respectively represent the $x$ and $y$ co-ordinate of the largest endpoint of the line segment.
- A method length that can be used to determine the length of a line segment. The length of a line segment is calculated as the Euclidean distance between both endpoints of the line segment.
Definie a class Rectangle with which rectangles can be represented in the Euclidean surface that have an area that is larger than zero. This class must support the following methods:
- An initializing method __init__ that allows to make a rectangle in the Euclidean surface based on two given vertices that are diametrically situated opposite each other. Two objects of the class Point must be given to this method, that represent the vertices that are diametrically opposite each other in the rectangle. The initializing method must appoint the attributes point1 and point2 of the newly made objects respectively the vertex in the left bottom corner and in the right upper corner. Watch the example below to verify which action the method should take if the given rectangle has an area of zero.
- Methods __str__ and __repr__ that both print the rectangle of the format "Rectangle(Point(x1, y1), Point(x2, y2))", where x1 and y1 respectively represent the $x$ and $y$ co-ordinate of a vertex in the left bottom corner of the rectangle and x2 and y2 respectively represent the $x$ and $y$ co-ordinates the vertex in the right upper corner of the rectangle.
- A method area that can be used to determine the area of the rectangle. The area of the rectangle is calculated as the product of the width of the rectangle.
- A method intersection that can be used to determine the intersection of two rectangles This method must print the value None if the rectangles don't intersect, or an object of the classes Point, Linesegment or Rectangle that describes the overlap of the two rectangle as a common vertex, a common side or a common rectangle.
Example
>>> p1 = Point(1, 2) >>> p1 Point(1, 2) >>> print(p1.x, p1.y) 1 2 >>> p2 = Point(3, 5) >>> print(p2) Point(3, 5) >>> p1 < p2 True >>> p1.distance(p2) 3.605551275463989 >>> l1 = Linesegment(Point(1,2), Point(3, 4)) >>> l1 Linesegment(Point(1, 2), Point(3, 4)) >>> print(l1.point1, l1.point2) Point(1, 2) Point(3, 4) >>> l1.length() 2.8284271247461903 >>> l2 = Linesegment(Point(5, -4), Point(-2, 3)) >>> print(l2) Linesegment(Point(-2, 3), Point(5, -4)) >>> l2.length() 9.899494936611665 >>> l3 = Linesegment(Point(1,2), Point(1, 2)) Traceback (most recent call last): AssertionError: line segment must have length larger than zero >>> r1 = Rectangle(Point(1, 1), Point(4, 4)) >>> r1 Rectangle(Point(1, 1), Point(4, 4)) >>> r1.area() 9 >>> r2 = Rectangle(Point(6, 3), Point(3, 6)) >>> r3 = Rectangle(Point(6, 3), Point(4, 2)) >>> print(r3) Rectangle(Point(4, 2), Point(6, 3)) >>> r3.area() 2 >>> r4 = Rectangle(Point(-7, -3), Point(1, 1)) >>> r1.intersection(r2) Rectangle(Point(3, 3), Point(4, 4)) >>> r1.intersection(r3) Linesegment(Point(4, 2), Point(4, 3)) >>> r2.intersection(r3) Linesegment(Point(4, 3), Point(6, 3)) >>> r1.intersection(r4) Point(1, 1) >>> r5 = Rectangle(Point(1, 1), Point(1, 1)) Traceback (most recent call last): AssertionError: rectangle must have area larger than zero
Als we de doorsnede van twee gegeven rechthoeken in het Euclidische vlak moeten bepalen, dan zijn er vier mogelijkheden. De doorsnede is ofwel leeg, een punt (gemeenschappelijk hoekpunt), een lijnstuk of een rechthoek.
Opgave
Definieer een klasse Punt waarmee punten in het Euclidische vlak met gehele coördinaten kunnen voorgesteld worden. Deze klasse moet ondersteuning bieden aan de volgende methoden:
- Een initialisatiemethode __init__ die toelaat om een punt in het Euclidische vlak aan te maken op basis van een $x$- en $y$-coördinaat. Beide coördinaten kunnen optioneel als de parameters x en y aan de initialisatiemethode doorgegeven worden ($x, y \in \mathbb{Z}$), en hebben de waarde nul indien ze niet worden opgegeven. De initialisatiemethode moet de opgegeven waarden of hun standaardwaarden respectievelijk toekennen aan de attributen x en y van het nieuw aangemaakte object.
- Methoden __str__ en __repr__ die beide een stringvoorstelling van een punt teruggeven onder de vorm "Punt(x, y)", waarbij x en y respectievelijk de $x$- en $y$-coördinaat van het punt in het Euclidische vlak voorstellen.
- Methoden __lt__, __le__, __eq__, __ne__, __gt__ en __ge__ die toelaten om twee punten uit het Euclidische vlak onderling te vergelijken aan de hand van de Python operatoren <, <=, ==, !=, > en >=. De vergelijking van twee punten gebeurt door eerst hun $x$-coördinaten te vergelijken, en daarna ook de $y$-coördinaten als de $x$-coördinaten gelijk zijn.
- Een methode afstand die kan gebruikt worden om de Euclidische afstand tussen twee punten in het Euclidische vlak te berekenen. De Euclidische afstand tussen twee punten $(x_1, y_1)$ en $(x_2, y_2)$ wordt gegeven door \[ \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \]
Definieer een klasse Lijnstuk waarmee lijnstukken in het Euclidische vlak kunnen voorgesteld worden die een lengte hebben groter dan nul. Deze klasse moet ondersteuning bieden aan de volgende methoden:
- Een initialisatiemethode __init__ die toelaat om een lijnstuk in het Euclidische vlak aan te maken op basis twee gegeven punten. Aan deze initialisatiemethode moeten twee objecten van de klasse Punt doorgegeven worden, die beide uiteinden van het lijnstuk voorstellen. Het kleinste van deze punten moet door de initialisatiemethode toegekend worden aan het attribuut punt1 van het nieuw aangemaakte object, en het grootste punt aan het attribuut punt2. Bekijk onderstaand voorbeeld om na te gaan welke actie de initialisatiemethode moet nemen indien het opgegeven lijnstuk lengte nul heeft.
- Methoden __str__ en __repr__ die beide een stringvoorstelling van het lijnstuk teruggeven onder de vorm "Lijnstuk(Punt(x1, y1), Punt(x2, y2))", waarbij x1 en y1 respectievelijk de $x$- en $y$-coördinaat van het kleinste eindpunt van het lijnstuk voorstellen en x2 en y2 respectievelijk de $x$- en $y$-coördinaat van het grootste eindpunt van het lijnstuk.
- Een methode lengte die kan gebruikt worden om de lengte van het lijnstuk te bepalen. De lengte van een lijnstuk wordt berekend als de Euclidische afstand tussen de twee eindpunten van het lijnstuk.
Definieer een klasse Rechthoek waarmee rechthoeken in het Euclidische vlak kunnen voorgesteld worden die een oppervlakte hebben groter dan nul. Deze klasse moet ondersteuning bieden aan de volgende methoden:
- Een initialisatiemethode __init__ die toelaat om een rechthoek in het Euclidische vlak aan te maken op basis twee gegeven hoekpunten die diametraal tegenover elkaar liggen. Aan deze initialisatiemethode moeten twee objecten van de klasse Punt doorgegeven worden, die diametraal tegenover elkaar liggende hoekpunten van de rechthoek voorstellen. De initialisatiemethode moet aan de attributen punt1 en punt2 van het nieuw aangemaakte object respectievelijk het hoekpunt in de linkeronderhoek en de rechterbovenhoek van de rechthoek toekennen. Bekijk onderstaand voorbeeld om na te gaan welke actie de initialisatiemethode moet nemen indien de opgegeven rechthoek oppervlakte nul heeft.
- Methoden __str__ en __repr__ die beide een stringvoorstelling van de rechthoek teruggeven onder de vorm "Rechthoek(Punt(x1, y1), Punt(x2, y2))", waarbij x1 en y1 respectievelijk de $x$- en $y$-coördinaat van het hoekpunt in de linkeronderhoek van de rechthoek voorstellen en x2 en y2 respectievelijk de $x$- en $y$-coördinaat van het hoekpunt in de rechterbovenhoek van de rechthoek.
- Een methode oppervlakte die kan gebruikt worden om de oppervlakte van de rechthoek te bepalen. De oppervlakte van een rechthoek wordt berekend als het product van de breedte en de hoogte van de rechthoek.
- Een methode doorsnede die kan gebruikt worden om de doorsnede van twee rechthoeken te bepalen. Deze methode moet de waarde None teruggeven indien de twee rechthoeken elkaar niet overlappen, of een object van de klasse Punt, Lijnstuk of Rechthoek dat de overlap van de twee rechthoeken omschrijft als een gemeenschappelijk hoekpunt, een gemeenschappelijke zijde of een gemeenschappelijke rechthoek.
Voorbeeld
>>> p1 = Punt(1, 2) >>> p1 Punt(1, 2) >>> print(p1.x, p1.y) 1 2 >>> p2 = Punt(3, 5) >>> print(p2) Punt(3, 5) >>> p1 < p2 True >>> p1.afstand(p2) 3.605551275463989 >>> l1 = Lijnstuk(Punt(1,2), Punt(3, 4)) >>> l1 Lijnstuk(Punt(1, 2), Punt(3, 4)) >>> print(l1.punt1, l1.punt2) Punt(1, 2) Punt(3, 4) >>> l1.lengte() 2.8284271247461903 >>> l2 = Lijnstuk(Punt(5, -4), Punt(-2, 3)) >>> print(l2) Lijnstuk(Punt(-2, 3), Punt(5, -4)) >>> l2.lengte() 9.899494936611665 >>> l3 = Lijnstuk(Punt(1,2), Punt(1, 2)) Traceback (most recent call last): AssertionError: lijnstuk moet lengte hebben die groter is dan nul >>> r1 = Rechthoek(Punt(1, 1), Punt(4, 4)) >>> r1 Rechthoek(Punt(1, 1), Punt(4, 4)) >>> r1.oppervlakte() 9 >>> r2 = Rechthoek(Punt(6, 3), Punt(3, 6)) >>> r3 = Rechthoek(Punt(6, 3), Punt(4, 2)) >>> print(r3) Rechthoek(Punt(4, 2), Punt(6, 3)) >>> r3.oppervlakte() 2 >>> r4 = Rechthoek(Punt(-7, -3), Punt(1, 1)) >>> r1.doorsnede(r2) Rechthoek(Punt(3, 3), Punt(4, 4)) >>> r1.doorsnede(r3) Lijnstuk(Punt(4, 2), Punt(4, 3)) >>> r2.doorsnede(r3) Lijnstuk(Punt(4, 3), Punt(6, 3)) >>> r1.doorsnede(r4) Punt(1, 1) >>> r5 = Rechthoek(Punt(1, 1), Punt(1, 1)) Traceback (most recent call last): AssertionError: rechthoek moet oppervlakte hebben die groter is dan nul
| Added by: | Peter Dawyndt |
| Date: | 2012-03-06 |
| Time limit: | 5s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | |
| Resource: | None |

 RSS
RSS