| Submit | All submissions | Best solutions | Back to list |
PROG0225 - Trilaterations |
Trilateration is the process of determining (relative) locations or points by measurement of distances from this point to a few other, known points. It is based on the geometric properties of circles. Unlike with triangluation, there is no measuring of angles in trilateration. This technique has a couple of very practical applications, such as the GPS system, determining the epicenter of an earthquake…
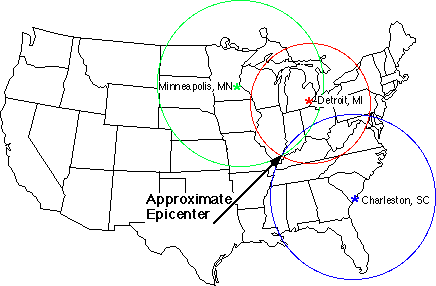
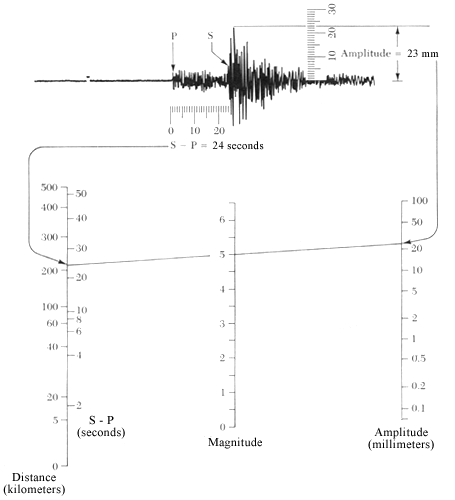
To determine the epicenter of an earthquake, for example, you can work as follows. You calculate the time between the first P-wave and the first S-wave for various weather stations. You can determine the distance from the epicenter to the weather station based on known tables. In the picture below you can see that a difference of 24 seconds between the first P-wave and the first S-wave corresponds with an epicenter in a 215 km radius. Now you can draw a circle around the area where the epicenter is situated. If you have multiple measuring points, you will find the epicenter in the intersection of multiple circles. In reality, there will always be a mistake in the measurement and the circles will never really intersect. You will however find an area of possibilities for the location of the epicenter.
An important feature of trilateration is determining the position of two circles. In the table below you will find an overview of the mutual positions possible for two circles. $d$ stands for the distance between the centres of both circles. $r_1$ and $r_2$ respectively stand for the radius of the first and the second circle.
| position | condition |
|---|---|
| concentric | $d=0$ |
| touching inside | $d=|r_1-r_2|$ |
| touching outside | $d=r_1+r_2$ |
| enclosing | $d < |r_1-r_2|$ |
| intersecting | $|r_1-r_2| < d < r_1+r_2$ |
| separate | $d > r_1+r_2$ |
The distance $d$ between two points $(x_1,y_1)$ and $(x_2,y_2)$ is calculated with the formula below:
$d = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}$.
Caution: If you work with real numbers on a computer, mistakes in rounding off occur very often. This is why 2 numbers that should be equal, often aren't. To fix this problem, we add a margin of error: we say that two numbers are equal if the difference between those two numbers is smaller than $10^{-2}$.
Input
The input consists of six real numbers: one number per line. The first line represents the $x$ co-ordinate of the first circle, followed by a line with the $y$ co-ordinate of the circle and a line with the circle's radius. Then, this is repeated with the quantities of the second circle.
Output
The output consists of a single line that contains one of six terms: concentric, touching inside, touching outside, enclosing, intersecting or separate. The term should state the mutual position of the two circles from the input.
Example
Input:
3.5 2.7 7.86 6.5 6.7 2.86
Output:
touching inside
Trilateratie is het bepalen van de (relatieve) positie van een punt aan de hand van de afstanden van dit punt tot enkele gekende punten. Hierbij wordt gesteund op de meetkundige eigenschappen van cirkels. In tegenstelling tot triangulatie worden er bij trilateratie geen hoeken gemeten. Deze techniek heeft enkele zeer praktische toepassingen zoals het GPS-systeem, het bepalen van het epicentrum van een aardbeving, …
Om bvb. het epicentrum van een aardbeving te bepalen kan je als volgt te werk gaan. Je bepaalt voor verschillende meetstation de tijd tussen de eerste P-golf en de eerste S-golf. Aan de hand van gekende tabellen kan je hieruit het afstand van het epicentrum tot het meetstation bepalen. Zo zie je op onderstaande afbeelding dat een verschil van 24 seconden tussen de eerste P-golf en de eerste S-golf correspondeert met een epicentrum op afstand 215 km. Dit geeft je dus een cirkel waarop het epicentrum kan liggen. Als je meerdere meetpunten hebt, dan wordt het epicentrum gegeven door het snijpunt van de verschillende cirkels. In werkelijkheid zal hier steeds een meetfout op zitten en zal je nooit echt een mooi snijpunt vinden, maar eerder een gebied van mogelijkheden.
Een belangrijk onderdeel van trilateratie is het bepalen van de onderlinge positie van twee cirkels. Hieronder zie je een overzicht van de mogelijke onderlinge posities van twee cirkels. In deze tabel staat $d$ voor de afstand tussen de middelpunten van de twee cirkels en $r_1$, respectievelijk $r_2$, voor de straal van de eerste, respectievelijk de tweede cirkel.
| positie | voorwaarde |
|---|---|
| concentrisch | $d=0$ |
| binnen rakend | $d=|r_1-r_2|$ |
| buiten rakend | $d=r_1+r_2$ |
| omsluitend | $d < |r_1-r_2|$ |
| snijdend | $|r_1-r_2| < d < r_1+r_2$ |
| gescheiden | $d > r_1+r_2$ |
De afstand $d$ tussen twee punten $(x_1,y_1)$ en $(x_2,y_2)$ wordt hierbij berekend aan de hand van de volgende formule:
$d = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}$.
Opgelet: Als je met reële getallen werkt op een computer, treden er al snel afrondingsfouten op. Hierdoor zullen twee getallen die gelijk zouden moeten zijn, vaak net niet gelijk zijn. Daarom voegen we een foutenmarge in: we zeggen dat twee getallen gelijk zijn, als het verschil tussen deze twee getallen kleiner is dan $10^{-2}$.
Invoer
De invoer bestaat uit zes reële getallen: één getal per regel. Op de eerste regel staat de $x$-coördinaat van de eerste cirkel, gevolgd door een regel met de $y$-coördinaat van de cirkel en een regel met de straal van de cirkel. Dan herhalen deze drie grootheden zich voor de tweede cirkel.
Uitvoer
De uitvoer bestaat uit één enkele regel die één van de volgende termen bevat: concentrisch, binnen rakend, buiten rakend, omsluitend, snijdend of gescheiden. De term die wordt uitgeschreven moet hierbij de onderlinge positie van de twee gegeven cirkels aangeven die via de invoer opgegeven werden.
Voorbeeld
Invoer:
3.5 2.7 7.86 6.5 6.7 2.86
Uitvoer:
binnen rakend
| Added by: | Peter Dawyndt |
| Date: | 2012-02-16 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | |
| Resource: | None |

 RSS
RSS