| Submit | All submissions | Best solutions | Back to list |
PROG0213 - Simulating polymers |
A self-avoiding walk (SAW) consists of a series of steps on a rectangle grid, where the same point is visited once at the most. SAWs were introduced by chemist Paul Flory for modelling the behaviour of chain-like structures such as solvents and polymers. The three-dimensional interpretation of such structures doesn't allow that the same point is occupied more than once. It is extremely difficult to deduct the properties of SAWs in a mathematical manner. However, chemists and physicists have deducted various patterns of macromolecules, where the conjecture of their validity is based on numeric simulations. Moreover, it delivered Flory the Nobel prize in chemistry in 1974.
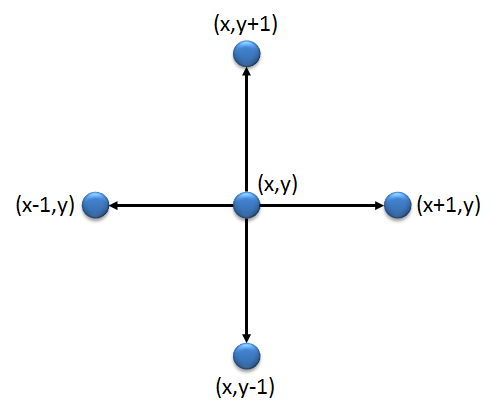
To be able to execute numeric simulations, we represent a polymer in a Cartesian surface as a sequence of monomers that are linked together based on the principle of a self-avoiding walk. We suppose that the first monomer is situated in the origin $(0,0)$ of that surface, and that the $x$ axis of the co-ordinate scale is pointed to the right, and the $y$ axis is pointing upwards. The next monomer in the sequence is always one unit above, under, left or right from the monomer before $(x,y)$, as illustrated in the picture below.
If we represent a position in the Cartesian surface as a tuple with two elements $(x,y)$, we can represent a polymer as a list of tuples, of which the first tuple represents the origin $(0,0)$.
Assignment
- Write a function grow that determines a position of the next monomer in a polymer for a monomer on a given position $(x,y)$ (where $x, y \in \mathbb{Z}$). This position must be chosen randomly from a number of possible positions above, under, left and right from the other monomer. Positions that are already taken by monomers of the polymer may not be chosen again. Two obligatory arguments must be given to the function. The first argument is a tuple with two elements that represent the position $(x,y)$ of the monomer before. The second argument is a check object that contains all positions (again, every position is represented as a tuple of two integers) that are already occupied by monomers of the polymer. As a result, the function must print one of the possible positions (again represented as a tuple of two elements) that lays around the position of the monomer before an has not yet been taken by other monomers of the polymer. If all four positions have already been taken, the function must print the value None as a result.
- Write a function polymer that prints a list of tuples with two elements as a result. This list represents a polymer, of which the tuples represent the positions of the monomers within that polymer. The first element of the list is the tuple $(0,0)$ that represents the origin of the Cartesian surface. Use the function grow to add the position of the next monomer based on the previous positions. Keep repeating this procedure until all four positions around the last position are taken an the polymer can't be expanded anymore.
Example
>>> grow((0, 0), [(1, 0), (-1, 0), (0, -1)]) (0, 1) >>> grow((0, 0), [(1, 0), (-1, 0), (0, 1)]) (0, -1) >>> grow((0, 0), [(1, 0), (0, 1), (0, -1)]) (-1, 0) >>> grow((0, 0), [(-1, 0), (0, 1), (0, -1)]) (1, 0) >>> grow((0, 0), [(1, 0), (-1, 0), (0, 1), (0, -1)])
>>> polymer() [(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (1, 2), (0, 2), (0, 1), (1, 1)] >>> polymer() [(0, 0), (1, 0), (2, 0), (2, -1), (3, -1), (4, -1), (4, 0), (4, 1), (3, 1), (3, 0)]
Een self-avoiding walk (SAW) bestaat uit een reeks stappen op een rechthoekig rooster, waarbij hetzelfde punt hoogstens één keer bezocht wordt. SAWs werden geïntroduceerd door de chemicus Paul Flory voor het modelleren van het gedrag van ketenachtige structuren zoals solventen en polymeren. De ruimtelijke invulling van dergelijk structuren laat immers niet toe dat hetzelfde punt meerdere keren bezet wordt. Het is extreem moeilijk om de eigenschappen van SAWs op een wiskundige manier af te leiden. Desondanks hebben chemici en natuurkundigen reeds verschillende wetmatigheden van macromoleculen afgeleid, waarbij het vermoeden van hun geldigheid berust op numerieke simulaties. Het leverde Flory in 1974 uiteindelijk ook de Nobelprijs in de scheikunde op.
Om numerieke simulaties te kunnen uitvoeren, stellen we een polymeer in het cartesisch vlak voor als een reeks monomeren die aaneengeschakeld worden volgens het principe van een self-avoiding walk. We veronderstellen daarbij dat het eerste monomeer in de oorsprong $(0,0)$ van het vlak ligt, en dat de $x$-as van het coördinatenstelsel naar rechts gericht is, en de $y$-as naar boven. Het volgende monomeer uit de reeks ligt telkens één eenheidsstap boven, onder, links of rechts van het vorige monomeer $(x,y)$, zoals geïllustreerd in onderstaande figuur.
Als we een positie in het cartesisch vlak voorstellen als een tuple met twee elementen $(x,y)$, dan kunnen we een polymeer voorstellen als een lijst van tuples, waarbij het eerste tuple de oorsprong $(0,0)$ voorstelt.
Opgave
- Schrijf een functie groei die voor een monomeer op een gegeven positie $(x,y)$ (waarbij $x, y \in \mathbb{Z}$), een positie voor het volgende monomeer in een polymeer bepaalt. Deze positie moet willekeurig gekozen worden uit de mogelijke posities boven, onder, links en rechts van het vorige monomeer. Posities die reeds door monomeren van het polymeer zijn ingenomen mogen hierbij niet opnieuw gekozen worden. Aan de functie moeten verplicht twee argumenten doorgegeven worden. Het eerste argument is een tuple met twee elementen dat de positie $(x,y)$ van het vorige monomeer aangeeft. Het tweede argument is een collectieobject dat alle posities (opnieuw wordt elke positie voorgesteld als een tuple van twee gehele getallen) bevat die reeds door monomeren van het polymeer zijn ingenomen. Als resultaat moet de functie één van de mogelijke posities (opnieuw voorgesteld door een tuple van twee elementen) teruggeven die rondom de gegeven positie ligt en die nog niet bezet is door een monomeer van het polymeer. Indien alle vier de posities rondom de gegeven positie reeds bezet zijn, dan moet de functie de waarde None als resultaat teruggeven.
- Schrijf een functie polymeer die een lijst van tuples met twee elementen als resultaat teruggeeft. Deze lijst stelt een polymeer voor, waarbij de tuples de posities van de verschillende monomeren van het polymeer voorstellen. Het eerste element van de lijst is het tuple $(0,0)$ dat de oorsprong van het cartesisch vlak voorstelt. Gebruik de functie groei om op basis van een vorige positie, telkens een volgende positie voor een monomeer achteraan de lijst toe te voegen. Blijf deze procedure herhalen totdat alle vier de posities rondom de laatste positie bezet zijn en het polymeer dus niet verder kan uitgebreid worden.
Voorbeeld
>>> groei((0, 0), [(1, 0), (-1, 0), (0, -1)]) (0, 1) >>> groei((0, 0), [(1, 0), (-1, 0), (0, 1)]) (0, -1) >>> groei((0, 0), [(1, 0), (0, 1), (0, -1)]) (-1, 0) >>> groei((0, 0), [(-1, 0), (0, 1), (0, -1)]) (1, 0) >>> groei((0, 0), [(1, 0), (-1, 0), (0, 1), (0, -1)]) >>> polymeer() [(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (1, 2), (0, 2), (0, 1), (1, 1)] >>> polymeer() [(0, 0), (1, 0), (2, 0), (2, -1), (3, -1), (4, -1), (4, 0), (4, 1), (3, 1), (3, 0)]
| Added by: | Peter Dawyndt |
| Date: | 2012-02-01 |
| Time limit: | 20s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | |
| Resource: | None |


 RSS
RSS