| Submit | All submissions | Best solutions | Back to list |
PROG0208 - Benfords law |
A jumble of numbers. As macroeconomic data comes across with most people. Just try to discover an irregularity or mistake. For years, the Greek government, could mislead the EU with its macroeconomic figures. The Greeks had discovered the seemingly perfect fraud: simple to implement and difficult to trace. The government presented its macroeconomic data, but adapted a annoying number here and there. The data was then sent to Eurostat, the European statistics agency, to prove that Greece fulfilled the Stability Pact of the EU. No questions asked, especially since checking macroeconomic data - summaries of complex economic processes - is a very complex task.
However, economists who control national accounts, are getting some unexpected help. A mathematical curiosity, called the law of Benford, seems to bring financial irregularities to light - without having to check numbers indefinitely. The law prescribes that in the initial digits of natural numbers intervals can be discovered. A wide range of data, from stocks to surfaces of lakes and primes to bids on eBay, all exhibit the same pattern. Surprisingly often the initial digit of such numbers is a 1, i.e. in about one in three numbers. Slightly less often is the initial digit 2, and even less often 3.
The "natural" distribution of leading digits
is defined in detail in the original 1937 article that describes the law
of Benford. It states that the probability $P (c)$ that a natural number
starts with the digit $c$ is equal to
\[
P(c) = \log_{10}\left(1 + \frac{1}{c}\right)
\]
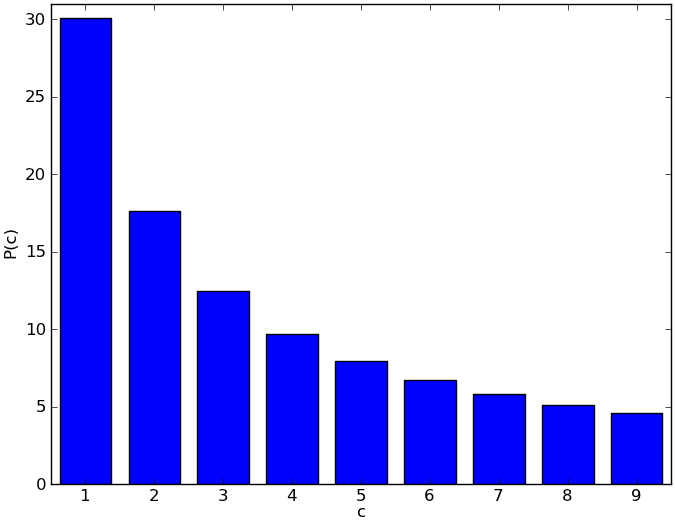
This probability is graphically shown in the figure below.
If a series of numbers deviates from this pattern, then the series is unlikely to have come about in a natural way and is possibly adjusted.
Assignment
- Write a function benford that returns the theoretical chance $P(c)$ that a natural number starts with the digit $c$. This chance must be expressed as a percentage. The digit $c$ must be passed to the function as an argument.
- Write a function readData, to which a file object must be passed as an obligatory argument. This file object must refer to an opened text file, of which all lines contains the same amount of information fields that are separated by one single dash. The function should return a list of integers, that contains the values of a given column of the text file. This column (field numbers are counted from 1) must be passed on as a second obligatory argument. If the given field of the text file contains real numbers, then these have to be rounded off to the closest integer value. Optionally, a third argument can be passed to the function: the dash that is used to separate the information fields in the text file. Use a tab as the default value for this optional argument.
- Write a function testBenford that can be used to check if a given list of integer values (that is passed to the function as an argument) meets the law of Benford. For each digit $c$ from 1 to 9 the function must print the first digit $c$ on a separate line, followed by the theoretical chance $P(c)$ (as percentage) that a natural number starts with the digit $c$ and the percentage of the integer values in the given list that start with the digit $c$. Both percentages are right aligned over 8 positions, and are rounded off to two decimal places.
Example
The file lakes.txt contains a list of all lakes in the American state Minnesota. Minnesota is sometimes called The Land of 10.000 Lakes, but an official count shows that there are about 11,842 lakes with a surface of 40,000 $\text{m}^2$. For each lake, the file contains the following information fields on a separate line, separated by a comma: i) name, ii) county, iii) nearby city, iv) total surface(in acres), v) surface littoral zone (in acres), vi) maximum depth (in feet) and vii) turbidity (in feet). For these data, the law of Benford still applies, as can be concluded from the interactive Python session below (with the surface of the littoral zone as an example).
>>> benford(3) 12.4938736608 >>> benford(7) 5.79919469777 >>> lakes = open('lakes.txt', 'r') >>> surface = readData(lakes, 5, ',') >>> surface [417, 269, 424, 238, 453, 2654, 96, ..., 1953, 367, 432, 345, 387, 89] >>> testBenford(surface) 1 30.10 31.81 2 17.61 20.55 3 12.49 12.51 4 9.69 9.29 5 7.92 6.61 6 6.69 6.17 7 5.80 5.00 8 5.12 4.47 9 4.58 3.57
Example
The following interactive Python session uses the file inhabitants.txt. This is the text file that consists of two columns (separated by a tab): i) the name and ii) the number of inhabitants of a state.
>>> inhabitants = open('inhabitants.txt', 'r') >>> data = readData(inhabitants, 2) >>> data [33609937, 3639453, 34178188, ..., 48508972, 9059651, 7604467] >>> testBenford(data) 1 30.10 25.11 2 17.61 16.88 3 12.49 11.69 4 9.69 14.29 5 7.92 5.19 6 6.69 8.23 7 5.80 7.36 8 5.12 6.93 9 4.58 4.33
Een wirwar van getallen. Zo komen macro-economische cijfers op de meeste mensen over. Zie daar maar eens een onregelmatigheid of een foutje in te ontdekken. Jarenlang kon de Griekse overheid de EU misleiden met haar macro-economische cijfers. De Grieken hadden de schijnbaar perfecte fraude ontdekt: simpel uit te voeren en moeilijk traceerbaar. De overheid stelde haar macro-economische gegevens vast, maar paste hier en daar een vervelend getal aan. De gegevens stuurden ze vervolgens naar Eurostat, het Europese statistiekagentschap, om te bewijzen dat Griekenland voldeed aan het stabiliteitspact van de EU. Geen haan die ernaar kraaide, vooral omdat het controleren van macro-economische cijfers — samenvattingen van complexe economische processen — een bijzonder ingewikkelde taak is.
Economen die nationale boekhoudingen controleren, krijgen echter hulp uit onverwachte hoek. Een wiskundige curiositeit, genaamd de wet van Benford, lijkt financieel gesjoemel genadeloos aan het licht te brengen — zonder getallen tot in den treure na te lopen. De wet schrijft voor dat in de begincijfers van natuurlijke getallen een bepaalde regelmaat is te ontdekken. De meest uiteenlopende gegevens, van aandelen tot oppervlakten van meren en van priemgetallen tot biedingen op eBay, allemaal vertonen ze hetzelfde patroon. Verrassend vaak is het begincijfer van dergelijke getallen een 1, namelijk bij ongeveer één op de drie getallen. Iets minder vaak is het begincijfer 2, nog iets minder vaak 3 enzovoort.
De 'natuurlijke' verdeling van begincijfers
is tot in detail vastgelegd in het originele artikel uit 1937 dat de wet
van Benford beschrijft. Hierin wordt gesteld dat de kans $P(c)$ dat een
natuurlijk getal begint met het cijfer $c$ gelijk is aan
\[
P(c) = \log_{10}\left(1 + \frac{1}{c}\right)
\]
Deze kans wordt grafisch weergegeven in onderstaande figuur.
Wijkt een reeks getallen van dit patroon af, dan is de reeks waarschijnlijk niet op een natuurlijke manier tot stand gekomen — of mogelijk aangepast.
Opgave
- Schrijf een functie benford die de theoretische kans $P(c)$ teruggeeft dat een natuurlijk getal begint met het cijfer $c$. Deze kans moet uitgedrukt worden als een percentage. Het cijfer $c$ moet als argument aan de functie doorgegeven worden.
- Schrijf een functie leesData, waaraan als eerste verplicht argument een bestandsobject moet doorgegeven worden. Dit bestandsobject moet verwijzen naar een geopend tekstbestand, waarvan alle regels eenzelfde aantal informatievelden bevatten die telkens van elkaar gescheiden worden door één enkel scheidingskarakter. De functie moet als resultaat de lijst van integerwaarden teruggeven, die de waarden uit een gegeven kolom van het tekstbestand bevat. Deze kolom (veldnummers worden geteld vanaf 1) moet als tweede verplicht argument aan de functie doorgegeven worden. Indien het opgegeven veld van het tekstbestand reële getallen bevat, dan moeten deze afgerond worden naar de dichtstbijzijnde integerwaarde. Optioneel kan een derde argument aan de functie doorgegeven worden: het scheidingskarakter dat gebruikt wordt om de informatievelden in het tekstbestand van elkaar te scheiden. Gebruik een tab als standaardwaarde voor dit optioneel argument.
- Schrijf een functie testBenford die kan gebruikt worden om na te gaan of een gegeven lijst van integerwaarden (die als argument aan de functie doorgegeven wordt) voldoet aan de wet van Benford. Voor elk cijfer $c$ van 1 tot en met 9 moet de functie op een afzonderlijk regel eerst het cijfer $c$ zelf uitschrijven, gevolgd door de theoretische kans $P(c)$ (als percentage) dat een natuurlijk getal begint met het cijfer $c$ en het percentage van de integerwaarden in de gegeven lijst die beginnen het cijfer $c$. Beide percentages worden telkens rechts uitgelijnd over 8 posities, en worden weergegeven afgerond tot op twee cijfers na de komma.
Voorbeeld
Het bestand meren.txt bevat een lijst van alle meren in de Amerikaanse staat Minnesota. Minnesota wordt ook wel The Land of 10.000 Lakes genoemd, maar een officiële telling geeft aan dat er ongeveer 11.842 meren zijn met een totale oppervlakte van 40.000 $\text{m}^2$. Voor elk meer bevat het bestand op een afzonderlijke regel de volgende informatievelden, die van elkaar gescheiden worden door een komma: i) naam, ii) provincie, iii) nabijgelegen stad, iv) totale oppervlakte (in acre), v) oppervlakte getijdenzone (in acre), vi) maximale diepte (in voet) en vii) troebelheid (in voet). Ook voor deze gegevens geldt de Wet van Benford, zoals blijkt uit onderstaande interactieve Pythonsessie (met de oppervlate van de getijdenzone als voorbeeld).
>>> benford(3) 12.4938736608 >>> benford(7) 5.79919469777 >>> meren = open('meren.txt', 'r') >>> oppervlakte = leesData(meren, 5, ',') >>> oppervlakte [417, 269, 424, 238, 453, 2654, 96, ..., 1953, 367, 432, 345, 387, 89] >>> testBenford(oppervlakte) 1 30.10 31.81 2 17.61 20.55 3 12.49 12.51 4 9.69 9.29 5 7.92 6.61 6 6.69 6.17 7 5.80 5.00 8 5.12 4.47 9 4.58 3.57
Voorbeeld
Onderstaande interactieve Pythonsessie maakt gebruik van het bestand inwoners.txt. Dit is een tekstbestand dat bestaat uit twee kolommen (van elkaar gescheiden door een tab): i) de naam en ii) het aantal inwoners van een land.
>>> inwoners = open('inwoners.txt', 'r') >>> data = leesData(inwoners, 2) >>> data [33609937, 3639453, 34178188, ..., 48508972, 9059651, 7604467] >>> testBenford(data) 1 30.10 25.11 2 17.61 16.88 3 12.49 11.69 4 9.69 14.29 5 7.92 5.19 6 6.69 8.23 7 5.80 7.36 8 5.12 6.93 9 4.58 4.33
| Added by: | Peter Dawyndt |
| Date: | 2012-01-31 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | |
| Resource: | None |

 RSS
RSS