| Submit | All submissions | Best solutions | Back to list |
PROG0099 - Improved linear interpolation |
We have already applied linear interpolation in a previous assignment to estimate the missing measurements of a function $y = f(x)$ on the basis of known measurements. We assumed that the function was measured for the $x$-values 1, 2, …, 100.
In this assignment we will extend this technique for a variable number of measurement points $x_i$ ($1 \leq i \leq n$) which do not necessarily coincide with the integers, and which may even have different distances between them. The only thing we assume is that $x_i < x_j$ is always valid if $i < j$, in other words, that increasing $x$-values were applied when measuring (or that the measurements were sorted in that order).
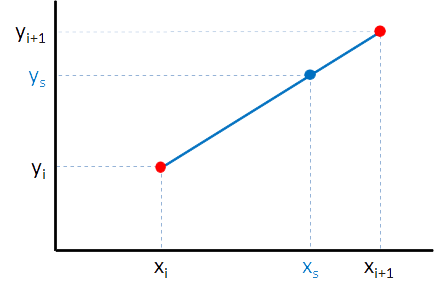
To estimate the value $y_s = f(x_s)$ which matches the $x$-value $x_s$ — which lies between the successive $x$-values $x_i$ and $x_{i+1}$ — we still use the formula for linear interpolation: \[ y_s = y_i + (x_s-x_i)\frac{(y_{i+1}-y_i)}{(x_{i+1}-x_i)} \]
Assignment
Write a function interpolation to which two arguments must be passed. The first argument is a list of measurement points, where each measurement point is represented as a tuple $(x, y)$ where $x, y \in \mathbb{R}$. The second argument is a number l $x_s \in \mathbb{R}$. If the $x$-values of the given measurement points are not give in ascending order, then the function should return the string 'invalid input'. If the given $x$-value $x_s$ is not within the range of the measurement points ($x_s < x_1$ of $x_s > x_n$), then the function should return the string 'out of range'. Otherwise the function should return the $y$-value $y_s \in \mathbb{R}$ that, according to the principle of linear interpolation, corresponds with the given $x$-value $x_s$.
Example
>>> interpolation([(4.88, -2.15), (6.42, -0.45), (6.99, 3.93), (7.69, -3.64)], 5.45) -1.5207792207792203 >>> interpolation([(3.3, 1.26), (4.25, -0.27), (6.17, 3.53), (8.16, 2.47)], 8.11) 2.496633165829146 >>> interpolation([(2.24, 1.66), (3.5, 0.43), (3.96, -0.57), (4.35, -0.25)], 5.56) 'out of range' >>> interpolation([(2.61, -1.97), (1.66, -0.05), (3.33, -0.93), (5.18, -0.58)], 7.1) 'invalid input'
We hebben lineaire interpolatie reeds in een vorige opgave toegepast om ontbrekende meetresultaten van een functie $y = f(x)$ te schatten op basis van gekende metingen. We hadden daarbij de veronderstelling gemaakt dat de functie werd gemeten bij de $x$-waarden 1, 2, …, 100.
In deze opgave zullen we deze techniek uitbreiden voor een variabel aantal meetpunten $x_i$ ($1 \leq i \leq n$) die niet noodzakelijk samenvallen met de natuurlijke getallen, en die zelfs niet langer even ver van elkaar moeten liggen. Het enige wat we veronderstellen is dat er steeds geldt dat $x_i < x_j$ indien $i < j$, of met andere woorden dat er gemeten werd voor stijgende $x$-waarden (of dat de metingen in die volgorde gesorteerd werden).
Om de waarde $y_s = f(x_s)$ te schatten die hoort bij een $x$-waarde $x_s$ — die tussen twee opeenvolgende $x$-waarden $x_i$ en $x_{i+1}$ in ligt — maken we nog steeds gebruik van de formule voor lineaire interpolatie: \[ y_s = y_i + (x_s-x_i)\frac{(y_{i+1}-y_i)}{(x_{i+1}-x_i)} \]
Opgave
Schrijf een functie interpolatie waaraan twee argumenten moeten doorgegeven worden. Het eerste argument is een lijst van meetpunten, waarbij elk meetpunt wordt voorgesteld als een tuple $(x, y)$ waarbij $x, y \in \mathbb{R}$. Het tweede argument is een getal $x_s \in \mathbb{R}$. Indien de $x$-waarden van de gegeven meetpunten niet in stijgende volgorde gegeven zijn, dan moet de functie de string 'ongeldige invoer' als resultaat teruggeven. Indien de gegeven $x$-waarde $x_s$ niet binnen het het bereik van de meetpunten ligt ($x_s < x_1$ of $x_s > x_n$), dan moet de functie de string 'buiten bereik' als resultaat teruggeven. Anders moet de functie als resultaat de $y$-waarde $y_s \in \mathbb{R}$ teruggeven die volgens het principe van de lineaire interpolatie correspondeert met de gegeven $x$-waarde $x_s$.
Voorbeeld
>>> interpolatie([(4.88, -2.15), (6.42, -0.45), (6.99, 3.93), (7.69, -3.64)], 5.45) -1.5207792207792203 >>> interpolatie([(3.3, 1.26), (4.25, -0.27), (6.17, 3.53), (8.16, 2.47)], 8.11) 2.496633165829146 >>> interpolatie([(2.24, 1.66), (3.5, 0.43), (3.96, -0.57), (4.35, -0.25)], 5.56) 'buiten bereik' >>> interpolatie([(2.61, -1.97), (1.66, -0.05), (3.33, -0.93), (5.18, -0.58)], 7.1) 'ongeldige invoer'
| Added by: | Peter Dawyndt |
| Date: | 2011-08-04 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | |
| Resource: | None |

 RSS
RSS