| Nộp bài | Các bài nộp | Làm tốt nhất | Về danh sách bài |
MINPATH - Tìm đường đi ngắn nhất - Min paths |
Trong lý thuyết đồ thị, bài toán đường đi ngắn nhất nguồn đơn là bài toán tìm một đường đi giữa hai đỉnh sao cho tổng các trọng số của các cạnh tạo nên đường đi đó là nhỏ nhất. Định nghĩa một cách hình thức, cho trước một đồ thị có trọng số (nghĩa là một tập đỉnh V, một tập cạnh E, và một hàm trong số có giá trị thực f : E → R), cho trước một đỉnh v thuộc V, tìm một đường đi P từ v tới mỗi đỉnh v' thuộc V sao cho
là nhỏ nhất trong tất cả các đường nối từ v tới v' . Bài toán đường đi ngắn nhất giữa mọi cặp đỉnh là một bài toán tương tự, trong đó ta phải tìm các đường đi ngắn nhất cho mọi cặp đỉnh v và v' .
Các thuật toán quan trọng nhất giải quyết bài toán này là:
Thuật toán Dijkstra — giải bài toán nguồn đơn nếu tất cả các trọng số đều không âm. Thuật toán này có thể tính toán tất cả các đường đi ngắn nhất từ một đỉnh xuất phát cho trước s tới mọi đỉnh khác mà không làm tăng thời gian chạy.
Thuật toán Bellman-Ford — giải bài toán nguồn đơn trong trường hợp trọng số có thể có giá trị âm.
Giải thuật tìm kiếm A* giải bài toán nguồn đơn sử dụng heuristics để tăng tốc độ tìm kiếm
Thuật toán Floyd-Warshall — giải bài toán đường đi ngắn nhất cho mọi cặp đỉnh.
Thuật toán Johnson — giải bài toán đường đi ngắn nhất cho mọi cặp đỉnh, có thể nhanh hơn thuật toán Floyd-Warshall trên các đồ thị thưa.
Lý thuyết nhiễu (Perturbation theory); tìm đường đi ngắn nhất địa phương (trong trường hợp xấu nhất)
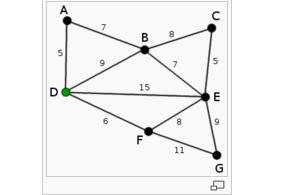
Ta xét bài toán đơn giản:
Cho đơn đồ thị vô hướng liên thông G = (V, E) gồm n đỉnh và m cạnh, các đỉnh được đánh số từ 1 tới n và các cạnh được đánh số từ 1 tới m, và 2 đỉnh s, t
Tìm đường đi ngắn nhất từ s đến t
Input
Dòng 1: Chứa 4 số n, m, s, t .
M dòng tiếp theo: Dòng thứ i có dạng ba số nguyên u, v, c. Trong đó u, v là chỉ số hai đỉnh đầu mút của cạnh thứ i và c trọng số của cạnh đó .
Output
Dòng 1: Ghi ra độ dài đường đi ngắn nhất
Dòng 2: Ghi ra thứ tự các đỉnh trên đường đi từ s đến t.
Example
Input: 3 3 1 3 1 2 3 2 3 1 1 3 5 Output: 4 1 2 3 Giới hạn: 1 <= n <= 100 1 <= m <=n(n-1)/2 |C| <= 10000
| Được gửi lên bởi: | special_one |
| Ngày: | 2009-01-04 |
| Thời gian chạy: | 1s |
| Giới hạn mã nguồn: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Ngôn ngữ cho phép: | C CSHARP CPP JAVA PAS-FPC |
hide comments
|
2021-04-26 09:41:16
Phạm Duy 1 đấm AC Last edit: 2021-04-26 09:42:11 |
|
|
2020-07-22 11:13:32
nhật hào bẩn |
|
|
2013-02-06 06:39:23 Trần Vãn Dương D10CN2
AO |

 RSS
RSS