| Nộp bài | Các bài nộp | Làm tốt nhất | Về danh sách bài |
BD2509 - Bao đóng truyền ứng |
Với đồ thị G = (V, E) ta xây dựng đồ thị mới G' = (E, V') cũng gồm các đỉnh của V nhưng các cạnh thì được xây dựng như sau:
Giữa 2 đỉnh u, v của G' có cạnh nối <=> có đường đi từ u đến v trong G.
Biểu diễn tập cạnh V của G bằng ma trận kề:
Aij = 1/0 tương ứng giữa 2 đỉnh i, j có/không có cạnh nối. (Aij = Aji)
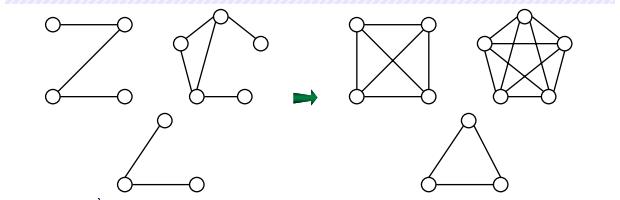
Bài toán: Cho G = (E, V). Tìm G' = (E, V')
Input
Dòng đầu tiên ghi số nguyên n ( 1 <= n <= 100 )
n dòng tiếp theo mô tả ma trận kề của đồ thị G. Dòng thứ i gồm n số. Số thứ j dòng thứ i là Aij.
Output
Gồm n dòng mô tả ma trận kề của đồ thị G'. Dòng thứ i gồm n số. Số thứ j dòng thứ i là A'ij.
Example
Input: 5 0 1 0 0 0 1 0 1 0 0 0 1 0 1 0 0 0 1 0 1 0 0 0 1 0 Output: 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0
| Được gửi lên bởi: | special_one |
| Ngày: | 2009-01-04 |
| Thời gian chạy: | 1s |
| Giới hạn mã nguồn: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Ngôn ngữ cho phép: | C CSHARP CPP JAVA PAS-FPC |

 RSS
RSS