| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
AL_27_07 - Trzeci ogród króla |
Król Bajtolomeusz zapragnął mieć nowy ogród, po którym mógłby w spokoju spacerować (o innych jego ogrodach można przeczytać tu i tu).
Ten nowy ogród ma kształt kwadratu i przecina go N ścieżek biegnących z południa na północ oraz tyle samo ścieżek biegnących z zachodu na wschód. Dodatkowo wytyczono ścieżki biegnące pomiędzy skrzyżowaniami z południowego-zachodu na północny-wschód.
W centralnym punkcie parku ustawiono fontannę i z tego powodu istnieją fragmenty ścieżek w jej bezpośrednim sąsiedztwie, którymi nie można przejść. Na poniższych rysunkach przedstawiono plany ogrodów dla N=3 i N=4, a niedostępne fragmenty ścieżek oznaczono kolorem czerwonym.
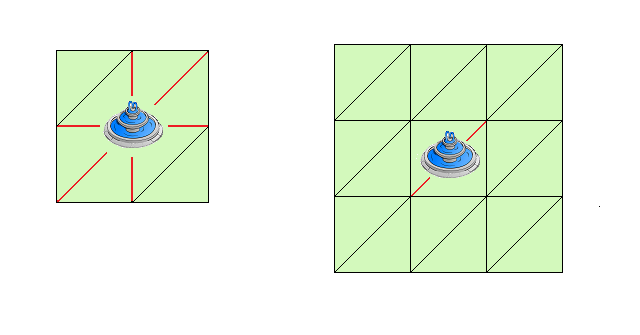
Król bardzo lubi przechadzać się po ogrodzie i spacer zaczyna zawsze w południowo-zachodnim narożniku a kończy go w narożniku północno-wschodnim. Podczas spaceru król porusza się wzdłuż ścieżek tylko na wschód, na północ lub na północny-wschód.
Bajtlomeusz chciałby wiedzieć, na ile różnych sposobów, będzie mógł odbyć spacer po swoim nowym ogrodzie. Ponieważ liczba ta może być bardzo duża, Bajtolomeusza interesuje jedynie reszta z dzielenia jej przez 1000000007.
Wejście
W pierwszej linii liczba testów t (1 ≤ t ≤ 2·105).
Dla każdego testu, w osobnej linii, jedna liczba całkowita N (2 ≤ N ≤ 106) oznaczająca liczbę ścieżek biegnących z południa na północ (i jednocześnie liczbę ścieżek biegnących z zachodu na wschód).
Wyjście
Dla każdego testu, w osobnej linii liczba możliwych spacerów króla Bajtolomeusza modulo 1000000007.
Przykład
Wejście: 3
2
3
4
Wyjście:
2
4
54
| Dodane przez: | Witold Długosz |
| Data dodania: | 2016-04-25 |
| Limit czasu wykonania programu: | 2s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: ASM64 GOSU JS-MONKEY |


 RSS
RSS