| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
AL_14_11 - Plansza |
 Marek i Czarek rozpoczynają grę planszową. Zaczynają w polu 0 (START) i muszą dojść do pola n (META). W każdej kolejce rzucają raz standardową kostką sześcienną i przemieszczają się pionkiem do przodu o wyrzuconą liczbę oczek. Zwycięża ten z zawodników, który dojdzie pierwszy do mety. Aby dojść do pola META, w ostatnim rzucie gracz musi wyrzucić liczbę oczek potrzebną do przesunięcia pionka do mety lub większą. Na niektórych polach są bonusy (np. przesuwasz się do przodu o określoną liczbę pól) albo kary (cofasz się do tyłu o pewną liczbę pól albo tracisz kolejkę). Jeżeli po 1000 kolejkach (wliczając w to ewentualne straty kolejek) nie ma roztrzygnięcia, to gracze tracą cierpliwość i ogłaszają remis. W pewnym momencie Marek i Czarek zaczęli się sprzeczać. Marek twierdzi, że gracz rozpoczynający pierwszy ma dużo większe szanse wygrać natomiast Czarek twierdzi, że nie ma to większego znaczenia. Kto z nich ma rację? Roztrzygnij ten spór.
Marek i Czarek rozpoczynają grę planszową. Zaczynają w polu 0 (START) i muszą dojść do pola n (META). W każdej kolejce rzucają raz standardową kostką sześcienną i przemieszczają się pionkiem do przodu o wyrzuconą liczbę oczek. Zwycięża ten z zawodników, który dojdzie pierwszy do mety. Aby dojść do pola META, w ostatnim rzucie gracz musi wyrzucić liczbę oczek potrzebną do przesunięcia pionka do mety lub większą. Na niektórych polach są bonusy (np. przesuwasz się do przodu o określoną liczbę pól) albo kary (cofasz się do tyłu o pewną liczbę pól albo tracisz kolejkę). Jeżeli po 1000 kolejkach (wliczając w to ewentualne straty kolejek) nie ma roztrzygnięcia, to gracze tracą cierpliwość i ogłaszają remis. W pewnym momencie Marek i Czarek zaczęli się sprzeczać. Marek twierdzi, że gracz rozpoczynający pierwszy ma dużo większe szanse wygrać natomiast Czarek twierdzi, że nie ma to większego znaczenia. Kto z nich ma rację? Roztrzygnij ten spór.
Wejście
W pierwszej linii wejścia podany jest rozmiar planszy n (1<=n<=1000). W drugiej linii podany jest ciąg n+1 liczb całkowitych (oddzielonych spacjami) opisujących kolejne pola planszy (od startu do mety):
- liczba 0 to pole zwykłe
- liczba z przedziału <-100, 100> oznacza przesunięcie pionka o określoną liczbę pól do przodu (wartość dodatnia) lub do tyłu (wartość ujemna)
- liczba 111 oznacza stratę kolejki przez danego gracza
Wiadomo, że start i meta są polami zwykłymi, natomiast z pól oznaczających przesunięcie pionek trafia zawsze na pole zwykłe.
Wyjście
W jedynej linii wyjścia należy podać dwie liczby (z dokładnością do 6 miejsc po przecinku) oznaczające odpowiednio: prawdopodobieństwo wygranej gracza rozpoczynającego grę oraz prawdopodobieństwo wygrania jego rywala.
Przykład
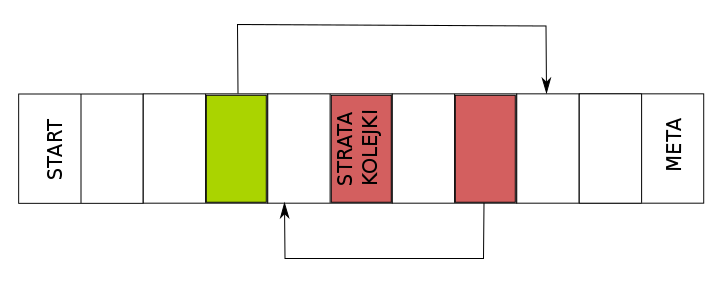
Wejście: 10
0 0 0 5 0 111 0 -3 0 0 0
Wyjście: 0.617678 0.382322
Plansza z przykładu:
| Dodane przez: | Ostry |
| Data dodania: | 2014-02-09 |
| Limit czasu wykonania programu: | 1s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: ASM64 GOSU |
ukryj komentarze
|
2014-02-16 10:26:25 Ostry
Chyba, że miałeś na myśli przesunięcie związane z polem bonusowym - każde takie przesunięcie odbywa się tylko w obrębie planszy |
|
|
2014-02-16 08:44:39 Ostry
Jeżeli rzut kostką jest większy lub równy niż ten potrzebny do osiągnięcia METY, to powoduje to osiągnięcie METY. Zdanie "Aby dojść do pola META, w ostatnim rzucie gracz musi wyrzucić liczbę oczek potrzebną do przesunięcia pionka do mety lub większą." to wyjaśnia. |
|
|
2014-02-16 00:49:25 Karol Ró¿ycki
Czy przesunięcie pionka może prowadzić go poza planszę? |

 RSS
RSS