| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
AL_13_12 - Skomplikowane układy profesora Algobita |
Od pewnego czasu profesor Algobit zajmuje się konstrukcją nowego super szybkiego i bardzo wydajnego procesora. Do budowy liczników, rejestrów i innych elementów procesora, profesor używa tylko czterech rodzajów bramek: XOR, NOR, NAND oraz NOT. Dodatkowo bramki NOR i NAND mają dowolną ilość wejść większą od 1, bramki XOR zawsze tylko dwa oraz NOT jedno wejście. Oczywiście każda z bramek ma tylko jedno wyjście. Naukowiec jest właśnie w fazie testowania swojego wynalazku, ale niestety nie jest to łatwe zadanie z prostej przyczyny - ilość bramek sięga nawet 100 000. Jeśli chcesz, aby twoje nazwisko pojawiło się w podziękowaniach publikacji profesora Algobita na temat tego wynalazku, napisz program, który pomoże testować ten skomplikowany układ cyfrowy.
Dla danego układu logicznego zbudowanego z bramek XOR, NOR, NAND oraz NOT określ jaki będzie stan wyjść dla danego stanu wejść.
Wejście
W pierwszym wierszu trzy liczby in, out i b określające odpowiednio ilość wejść, wyjść i bramek logicznych (1 ≤ in, out, b ≤ 105).
W drugim wierszu b bramek logicznych oddzielonych spacjami w formacie:
- NOT
- XOR
- NOR
- NAND
Pierwsza bramka podana w drugim wierszu ma numer 1, druga 2, ..., ostatnia b. Bramka NOT ma dokładnie jedno wejście, XOR dwa wejścia, natomiast NOR i NAND mają dowolną ilość wejść. Każda z bramek ma dokładnie jedno wyjście.
W trzecim wierszu jedna liczba p określająca ilość połączeń między elementami układu (p ≤ 106). W następnych p wierszach połączenia w jednym z czterech następujących formatów:
- format nr 1: numer bramki - numer bramki, np. 1 2 5
- format nr 2: numer wejścia - numer bramki, np. 2 in 1 5
- format nr 3: numer bramki - numer wyjścia, np. 3 4 out 2
- format nr 4: numer wejścia - numer wyjścia, np. 4 in 4 out 5
Następnie jedna liczba q określająca ilość zapytań (q ≤ 300 000). Każde zapytanie jest jednym z dwóch formatów:
- in numer wejścia zmiana stanu wejścia np. in 3
- out numer wyjścia np. out 100
W pierwszym zapytaniu należy zmienić stan wejścia na przeciwny, natomiast w drugim należy wyświetlić aktualny stan wyjścia.
Układ nie ma sprzężeń zwrotnych.
Wyjście
Dla każdego zapytania, które jest wyjściem, należy wypisać w osobnym wierszu jego stan: 0 - niski, 1 - wysoki. Na początku działania układu, wszystkie wejścia mają stan niski.
Przykład
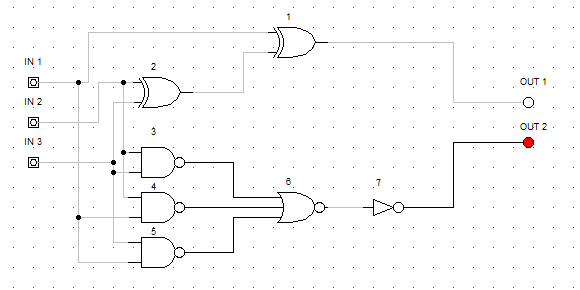
Wejście: 3 2 7 XOR XOR NAND NAND NAND NOR NOT 16 1 2 1 2 in 1 1 2 in 1 4 2 in 1 5 2 in 2 2 2 in 2 3 2 in 2 4 2 in 3 2 2 in 3 3 2 in 3 5 1 3 6 1 4 6 1 5 6 1 6 7 3 7 out 2 3 1 out 1 10 in 1 in 2 out 1 out 2 in 3 out 2 in 3 in 1 out 1 out 2
Wyjście: 0 1 0 1 1
Powyższy przykład prezentuje następujący układ:
| Dodane przez: | Marcin Kasprowicz |
| Data dodania: | 2013-11-27 |
| Limit czasu wykonania programu: | 1s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: ASM64 GOSU |
ukryj komentarze
|
2013-12-21 21:45:30 Marcin Kasprowicz
Zgadza się |
|
|
2013-12-21 21:39:43 Kamil Debowski
Brak sprzężeń zwrotnych nie zapewnia tego, że między dwoma wierzchołkami jest maksymalnie jedna ścieżka? |

 RSS
RSS