| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
AL_05_09 - Zamki z piasku |
 Plaża ciągnęła się w obie strony w nieskończoność pasem o stałej szerokości. Ograniczał ją tylko idealnie prosty brzeg morza z jednej strony i równoległa do niego linia wysokich drzew z drugiej. Z pobliskiego kempingu dochodziły odgłosy spędzających tu wakacje turystów. Jednak przy dzisiejszej niezbyt ładnej pogodzie, plaża świeciła pustkami. W pobliżu widać było tylko dwóch, zaskakująco podobnych do siebie, chłopców "uzbrojonych" w łopatki i wiaderka.
Plaża ciągnęła się w obie strony w nieskończoność pasem o stałej szerokości. Ograniczał ją tylko idealnie prosty brzeg morza z jednej strony i równoległa do niego linia wysokich drzew z drugiej. Z pobliskiego kempingu dochodziły odgłosy spędzających tu wakacje turystów. Jednak przy dzisiejszej niezbyt ładnej pogodzie, plaża świeciła pustkami. W pobliżu widać było tylko dwóch, zaskakująco podobnych do siebie, chłopców "uzbrojonych" w łopatki i wiaderka.
- Tylko nie wchodź na mój teren! - powiedział zdecydowanym głosem Franek do swojego brata bliźniaka.
- Ani ty na mój! - zrewanżował się Stefan. - I nie podglądaj. - dodał i chłopcy zaczęli budowę dwóch zamków z piasku.
Wcześniej ustalili, że, aby było sprawiedliwie, wybudują zamki w takiej samej odległości od brzegu morza. Dodatkowo, podzielili plażę na dwa królestwa, wytyczając prostą granicę. Tworzyły ją punkty jednakowo odległe od obu zamków.
Budowa szła całkiem sprawnie, zamki były coraz większe, gdy nagle Stefan zauważył, że ktoś zbliża się od strony kempingu.
- Patrz Franek! Ktoś tu idzie. - powiedział.
Franek spojrzał w tym samym kierunku, wytężył wzrok i rozpoznał nadchodzącą postać.
- No tak. To Janek. Można się było spodziewać, że w końcu nas znajdzie.
Janek był młodszym bratem bliźniaków. Chłopcom jednak nie zawsze zależało na wspólnym spędzaniu z nim czasu.
- Mama powiedziała, że mam się z wami bawić. - wypalił od razu Janek, gdy tylko zbliżył się do braci.
Bliźniakom się to nie uśmiechało, ale cóż było zrobić - skoro mama kazała, trzeba było smarkacza dopuścić do zabawy.
- Dobra! Możesz wybudować sobie swój zamek, ale nie może być bliżej brzegu niż nasze. - powiedział Franek.
- I w jednakowej odległości od obu naszych zamków! - dodał stanowczo Stefan.
- Właśnie. I nie przekraczaj granicy, bo jak podejdziesz za blisko, to dostaniesz. - uzupełnił bliźniak - Twoja będzie tylko ta część plaży, skąd do twojego zamku będzie bliżej niż do naszych. To będzie twoje królestwo.
Bliźniacy spojrzeli na siebie porozumiewawczo. Przy warunkach jakie postawili, młodszy brat na pewno nie będzie miał dużego królestwa - pomyśleli.
Jednak Janek, choć młodszy, był całkiem sprytny. Na budowę zamku wybrał takie miejsce, które oczywiście spełniało warunki postawione przez braci, ale powierzchnia stworzonego królestwa była największa z możliwych do uzyskania.
Podsumowując zadanie bardziej formalnie.
Plaża ma kształt "prostokąta" o stałej szerokości i nieskończonej długości. Franek i Stefan budują swoje zamki w dwóch różnych punktach na plaży, jednakowo odległych od brzegu morza (wymiary zamków zaniedbujemy). Janek może postawić swój zamek na plaży nie bliżej brzegu niż bracia. Odległość od jego zamku do zamku Franka musi być równa odległości do zamku Stefana. Królestwo każdego chłopca to zbiór takich punktów plaży, których odległość od jego zamku jest mniejsza niż odległości od zamków obu braci.
Poniższy rysunek przedstawia fragment plaży, na której chłopcy budują swoje zamki. Po wskazaniu rysunku myszką, można zobaczyć przykładowy podział plaży na królestwa, po wybudowaniu zamku przez Janka.
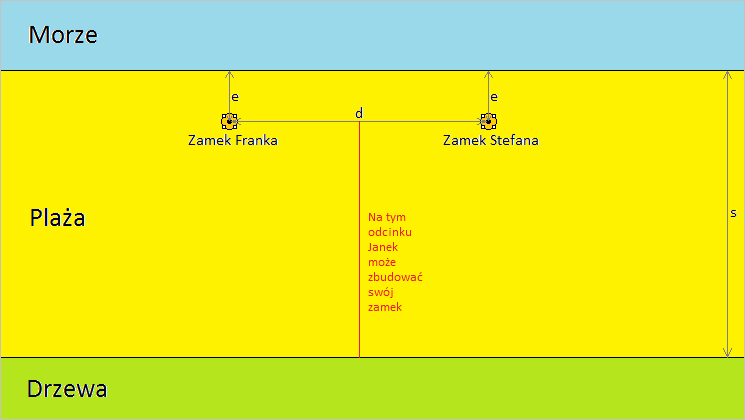
Znając szerokość plaży s, odległość pomiędzy zamkami bliźniaków d i odległość od każdego z tych zamków do brzegu e, oblicz maksymalną powierzchnię królestwa, jaką może uzyskać Janek, budując swój zamek w odpowiednim miejscu.
Wejście
W pierwszej linii liczba przypadków testowych t (1 ≤ t ≤ 100000).
W każdej z kolejnych t linii trzy liczby rzeczywiste s, e i d oznaczające odpowiednio: szerokość plaży (0 < s ≤ 100), odległość od zamku Franka (Stefana) do brzegu morza (0 ≤ e < s) i odległość pomiędzy zamkami bliźniaków (0 < d ≤ 2000). Liczby te podane są z dokładnością do co najwyżej trzech miejsc po przecinku.
Wyjście
Dla każdego przypadku testowego, w osobnej linii, jedna liczba rzeczywista oznaczająca maksymalne pole powierzchni jakie może mieć królestwo Janka, gdy ten wybuduje swój zamek we właściwym miejscu.
Wynik będzie uznany za prawidłowy, jeżeli błąd bezwzględny nie przekroczy 0.01.
Innymi słowy: jeśli wzorcowy wynik oznaczymy jako A, a wynik generowany przez program jako B, to test zostanie zaliczony, jeśli |A-B| ≤ 0.01.
Przykład
Wejście: 5
7 2 4
7 2 4
7 2 4
5 0 6.2
52.6 50.0 4.6 Wyjście: 26.065
26.06
26.07
25.581
120.980
Wyjaśnienie do przykładu: Trzy pierwsze przypadki testowe są takie same, ale choć wyniki różnią się od siebie, każdy zostanie uznany za poprawny, bo błąd nie przekracza dopuszczalnej wartości.
| Dodane przez: | Witold Długosz |
| Data dodania: | 2013-04-03 |
| Limit czasu wykonania programu: | 1s-4s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: ASM64 GOSU |
| Pochodzenie: | ALGOLIGA |
ukryj komentarze
|
2013-04-06 18:59:25 narbej
UWAGA! UWAGA! Proszę ;-) Nie róbcie edycji swoich wcześniejszych wiadomości - mogę ich nie zauważyć. Zawsze, jeżeli chcecie żebym je łatwiej zauważył, piszcie nowe. Ostatnio edytowany: 2013-04-06 19:19:27 |
|
|
2013-04-06 16:53:14 narbej
Tak |
|
|
2013-04-06 16:50:19 Andrzej Golonka
Czy królestwo Janka może może mieć swoją górną granicę która jest w mniejszej odległości od morza niż e? |

 RSS
RSS