| Zgłaszanie | Wszystkie zgłoszenia | Najlepsze | Lista |
AL_02_03 - Podział liczby |
W kombinatoryce rozważamy sposoby podziału obiektów na różne kategorie. Zarówno obiekty jak i kategorie mogą być rozróżnialne, bądź nie. Najtrudniejszym do zliczenia, ale i najciekawszym, przypadkiem jest gdy obiekty i kategorie są nierozróżnialne. Możemy o tym myśleć jako o rozkładzie liczby naturalnej n na sumę dodatnich całkowitych składników. Obiektami w tym przypadku niech będzie n jednakowych piłeczek, a kategoriami - rzędy do których je wkładamy. Kolejność rzędów nie jest istotna. Przydatnym, choć z pozoru trywialnym, narzędziem w zliczaniu takich podziałów są diagramy Ferrersa. Wizualnie przedstawiają one właśnie piłeczki ustawione w rzędach z narzuconą kolejnością - rzędy są posortowane względem liczby piłeczek.
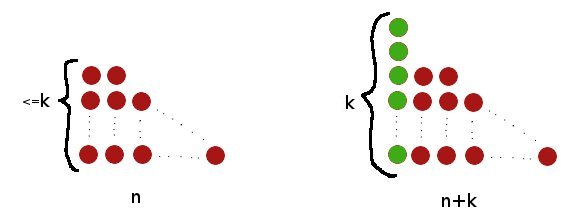
Przykładowo możemy bez trudu udowodnić, że liczba podziałów n na nie więcej niż k składników jest równa liczbie podziałów n+k na dokładnie k składników. Do każdego diagramu, który reprezentuje podział liczby n na nie więcej niż k składników, dostawiamy kolumnę k piłeczek. Otrzymujemy wtedy podział liczby n+k na dokładnie k składników. Takie przyporządkowanie jest wzajemnie jednoznaczne.
Nie jest łatwe policzenie wszystkich podziałów n, ale możemy rozważać szczególne podziały liczby dla których to zadanie jest łatwiejsze. Ciekawym przypadkiem podziału liczby jest jej rozkład na sumę kolejnych liczb naturalnych, co jest przedmiotem tego zadania.
Wejście
Wejście rozpoczyna się liczbą t<=1000 oznaczającą ilość przypadków testowych. Każdy przypadek testowy składa się z jednej liczby 1<=n<=106.
Wyjście
Dla każdego przypadku testowego należy wypisać w osobnej linii ilość podziałów liczby n na składniki będące kolejnymi liczbami naturalnymi.
Przykład
Wejście: 3
1
2
3 Wyjście: 1
1
2
Objaśnienie do przykładu - liczbę 3 możemy przedstawić na dwa sposoby jako sumę kolejnych liczb naturalnych:
3
1 + 2
| Dodane przez: | Adam Bąk |
| Data dodania: | 2012-09-29 |
| Limit czasu wykonania programu: | 0.100s-2.131s |
| Limit długości kodu źródłowego | 50000B |
| Limit pamięci: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Języki programowania: | All except: ASM64 GOSU |
| Pochodzenie: | ALGOLIGA |
ukryj komentarze
|
2012-11-03 14:36:59 Adam B±k
To, czy zero jest liczbą naturalną, czy też nie, jest kwestią umowy. Czasem jest, czasem nie. Umówmy się, że tutaj nie jest :-) |
|
|
2012-11-03 14:17:32 Przemek Komosa
czemu zero nie jest naturalne :P? |

 RSS
RSS