Bird tree

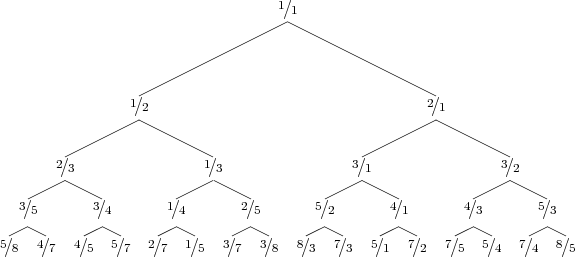
The Bird tree¹ is an infinite binary tree, whose first 5 levels look as follows:

It can be defined as follows:

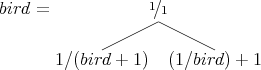
This is a co-recursive definition in which both occurrences of bird refer to the full (infinite) tree. The expression bird + 1 means that 1 is added to every fraction in the tree, and 1∕bird means that every fraction in the tree is inverted (so ^a∕_b becomes ^b∕_a).

Surprisingly, the tree contains every positive rational number exactly once, so every reduced fraction is at a unique place in the tree. Hence, we can also describe a rational number by giving directions (L for left subtree, R for right subtree) in the Bird tree. For example, ²∕₅ is represented by LRR. Given a reduced fraction, return a string consisting of L’s and R’s: the directions to locate this fraction from the top of the tree.

Input

On the first line a positive integer: the number of test cases, at most 100. After that per test case:

• one line with two integers a and b (1 ≤ a,b ≤ 10⁹), separated by a ’/’. These represent the numerator and denominator of a reduced fraction. The integers a and b are not both equal to 1, and they satisfy gcd(a,b) = 1.

For every test case the length of the string with directions will be at most 10 000.

Output

Per test case:

• one line with the string representation of the location of this fraction in the Bird tree.

Sample in- and output

3
1/2
2/5
7/3

L
LRR
RLLR

¹Hinze, R. (2009). The Bird tree. J. Funct. Program., 19:491–508.

Copyright notice

This problem text is copyright by the NWERC 2011 jury. It is licensed under the Creative Commons Attribution-Share Alike license version 3.0; The complete license text can be found at: http://creativecommons.org/licenses/by-sa/3.0/legalcode